제2장 : 통계 분석
먼저 데이터 분석을 수행할 환경의 경로를 설정합니다.
# Working Directory
setwd('C:/Users/wooil/Documents/GitHub/ADP')
getwd()
‘C:/Users/wooil/Documents/GitHub/ADP’
제2절 기초 통계 분석
1. 기술 통계
print(head(iris))
summary(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
Sepal.Length Sepal.Width Petal.Length Petal.Width
Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100
1st Qu.:5.100 1st Qu.:2.800 1st Qu.:1.600 1st Qu.:0.300
Median :5.800 Median :3.000 Median :4.350 Median :1.300
Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
Species
setosa :50
versicolor:50
virginica :50
# 평균, 중앙값, 표준편차, 분산, 1사분위수, 2사분위수, 3사분위수, 최댓값, 최솟값
print(mean(iris$Sepal.Length))
print(median(iris$Sepal.Length))
print(sd(iris$Sepal.Length))
print(var(iris$Sepal.Length))
print(quantile(iris$Sepal.Length, 1/4))
print(quantile(iris$Sepal.Length, 2/4))
print(quantile(iris$Sepal.Length, 3/4))
print(max(iris$Sepal.Length))
print(min(iris$Sepal.Length))
[1] 5.843333
[1] 5.8
[1] 0.8280661
[1] 0.6856935
25%
5.1
50%
5.8
75%
6.4
[1] 7.9
[1] 4.3
# MASS 패키지에 내장된 28가지 종의 동물 뇌의 무게와 몸무게 데이터
install.packages("MASS")
library(MASS)
Installing package into 'C:/Users/wooil/Documents/R/win-library/3.6'
(as 'lib' is unspecified)
package 'MASS' successfully unpacked and MD5 sums checked
The downloaded binary packages are in
C:\Users\wooil\AppData\Local\Temp\RtmpeQ9CHr\downloaded_packages
data("Animals")
print(head(Animals))
body brain
Mountain beaver 1.35 8.1
Cow 465.00 423.0
Grey wolf 36.33 119.5
Goat 27.66 115.0
Guinea pig 1.04 5.5
Dipliodocus 11700.00 50.0
summary(Animals)
body brain
Min. : 0.02 Min. : 0.40
1st Qu.: 3.10 1st Qu.: 22.23
Median : 53.83 Median : 137.00
Mean : 4278.44 Mean : 574.52
3rd Qu.: 479.00 3rd Qu.: 420.00
Max. :87000.00 Max. :5712.00
# 바디와 브레인의 사분위수 출력
print(quantile(Animals$body))
print(quantile(Animals$brain))
0% 25% 50% 75% 100%
0.023 3.100 53.830 479.000 87000.000
0% 25% 50% 75% 100%
0.400 22.225 137.000 420.000 5712.000
# 브레인/바디로 계산한 Ratio 변수 생성
Animals$ratio = Animals$brain/Animals$body
print(head(Animals))
body brain ratio
Mountain beaver 1.35 8.1 6.000000000
Cow 465.00 423.0 0.909677419
Grey wolf 36.33 119.5 3.289292596
Goat 27.66 115.0 4.157628344
Guinea pig 1.04 5.5 5.288461538
Dipliodocus 11700.00 50.0 0.004273504
회귀분석
1. 모형이 통계적으로 유의미한가?
F통계량을 확인한다. 유의수준 5% 하에서 F통계량의 p-값이 0.05보다 작으면 추정된 회귀식은 통계적으로 유의하다고 볼 수 있다.
2. 회귀계수들이 유의미한가?
해당 계수의 t통계량과 p-값 또는 이들의 신뢰구간을 확인한다.
3. 모형이 얼마나 설명력을 갖는가?
결정계수를 확인한다. 결정계수는 0에서 1값을 가지며, 높은 값을 가질수록 추정된 회귀식의 설명력이 높다.
4. 모형이 데이터를 잘 적합하고 있는가?
잔차를 그래프로 그리고 회귀진단을 한다.
5. 데이터가 아래의 모형 가정을 만족시키는가?
<가정>
- 선형성(독립변수의 변화에 따라 종속변수도 일정크기로 변화)
- 독립성(잔차와 독립변수의 값이 관련돼 있지 않음)
- 등분산성(독립변수의 모든 값에 대해 오차들의 분산이 일정)
- 비상관성(관측치들의 잔차들끼리 상관이 없어야 함)
- 정상성(잔차항이 정규분포를 이뤄야 함)
단순회귀분석
set.seed(2)
x = runif(10,0,11)
y = 2 + 3*x + rnorm(10, 0, 0.2)
dfrm = data.frame(x,y)
print(dfrm)
x y
1 2.033705 8.127599
2 7.726114 25.319934
3 6.306590 20.871829
4 1.848571 7.942608
5 10.382233 33.118941
6 10.378225 33.218204
7 1.420749 6.458597
8 9.167937 29.425272
9 5.148204 17.236677
10 6.049821 20.505909
plot(dfrm$x, dfrm$y)
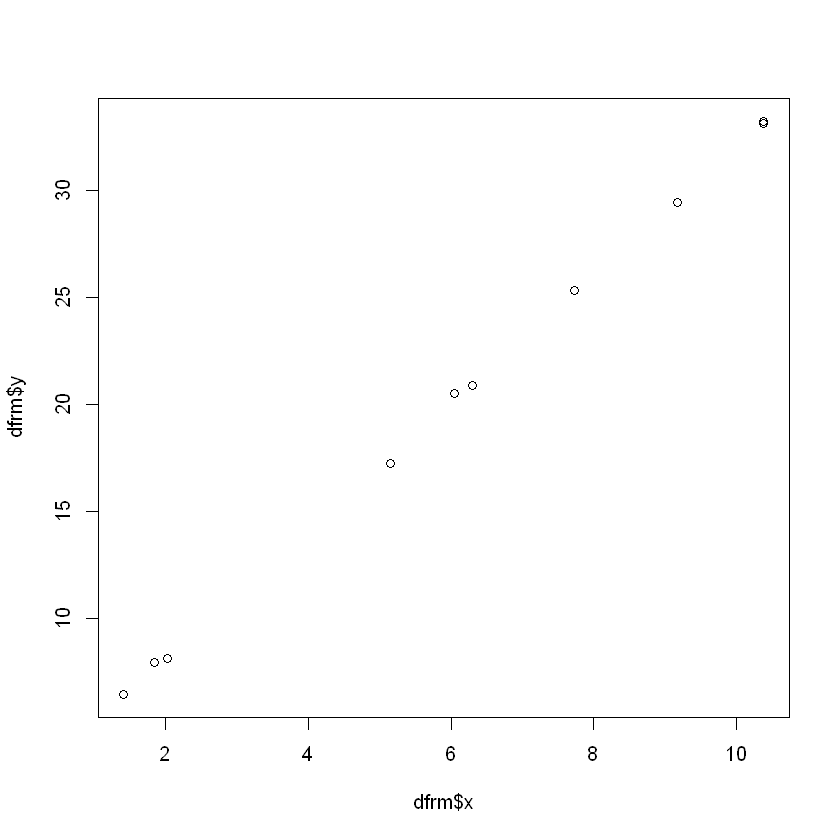
m <- lm(y~x, data=dfrm)
m
Call:
lm(formula = y ~ x, data = dfrm)
Coefficients:
(Intercept) x
2.213 2.979
summary(m)
Call:
lm(formula = y ~ x, data = dfrm)
Residuals:
Min 1Q Median 3Q Max
-0.311062 -0.118624 -0.002713 0.093296 0.272610
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.2133 0.1257 17.61 1.11e-07 ***
x 2.9786 0.0183 162.76 2.27e-15 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1885 on 8 degrees of freedom
Multiple R-squared: 0.9997, Adjusted R-squared: 0.9997
F-statistic: 2.649e+04 on 1 and 8 DF, p-value: 2.272e-15
다중회귀분석
set.seed(2)
u=runif(10,0,11)
v=runif(10,11,20)
w=runif(10,1,30)
y=3 + 0.1*u + 2*v - 3*w + rnorm(10,0, 0.1)
dfrm = data.frame(y,u,v,w)
print(dfrm)
y u v w
1 -25.6647952 2.033705 15.97407 20.195064
2 -6.5562326 7.726114 13.15005 12.238937
3 -36.4858791 6.306590 17.84462 25.269786
4 12.4472764 1.848571 12.62738 5.364542
5 0.1638434 10.382233 14.64754 11.070895
6 -3.9124946 10.378225 18.68194 15.174424
7 26.6127780 1.420749 19.78759 5.328159
8 -3.9238295 9.167937 13.03243 11.354815
9 -53.0331805 5.148204 15.00328 28.916677
10 12.4387413 6.049821 11.67481 4.838788
m<-lm(y~u+v+w)
m
Call:
lm(formula = y ~ u + v + w)
Coefficients:
(Intercept) u v w
3.0417 0.1232 1.9890 -2.9978
summary(m)
Call:
lm(formula = y ~ u + v + w)
Residuals:
Min 1Q Median 3Q Max
-0.188562 -0.058632 -0.002013 0.080024 0.143757
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.041653 0.264808 11.486 2.62e-05 ***
u 0.123173 0.012841 9.592 7.34e-05 ***
v 1.989017 0.016586 119.923 2.27e-11 ***
w -2.997816 0.005421 -552.981 2.36e-15 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.1303 on 6 degrees of freedom
Multiple R-squared: 1, Adjusted R-squared: 1
F-statistic: 1.038e+05 on 3 and 6 DF, p-value: 1.564e-14
결과
- F통계량:1.038e+05 p-값:1.564e-14 –> 유의수준 5% 하에서 추정된 회귀 모형이 통계적으로 매우 유의함.
- 결정계수 및 수정된 결정계수 모두 1로 이 회귀식이 데이터를 매우 잘 설명하고 있음.
- 회귀계수 u, v, w들의 p-값들도 0.01보다 작으므로 회귀계수의 추정치들이 유의수준 5% 하에서 통계적으로 유의함.
식이요법 방법을 적용한 닭에 대한 데이터
library(MASS)
data(ChickWeight)
print(head(ChickWeight))
weight Time Chick Diet
1 42 0 1 1
2 51 2 1 1
3 59 4 1 1
4 64 6 1 1
5 76 8 1 1
6 93 10 1 1
1번 닭에게 식이요법 방법 1을 적용한 데이터만 조회해 Chick 변수에 할당
Chick = ChickWeight[ChickWeight$Diet==1 & ChickWeight$Chick==1,]
print(Chick)
weight Time Chick Diet
1 42 0 1 1
2 51 2 1 1
3 59 4 1 1
4 64 6 1 1
5 76 8 1 1
6 93 10 1 1
7 106 12 1 1
8 125 14 1 1
9 149 16 1 1
10 171 18 1 1
11 199 20 1 1
12 205 21 1 1
시간의 경과에 따른 닭들의 몸무게를 단순회귀분석 시행
model = lm(weight ~ Time, Chick)
summary(model)
Call:
lm(formula = weight ~ Time, data = Chick)
Residuals:
Min 1Q Median 3Q Max
-14.3202 -11.3081 -0.3444 11.1162 17.5346
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 24.4654 6.7279 3.636 0.00456 **
Time 7.9879 0.5236 15.255 2.97e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 12.29 on 10 degrees of freedom
Multiple R-squared: 0.9588, Adjusted R-squared: 0.9547
F-statistic: 232.7 on 1 and 10 DF, p-value: 2.974e-08
plot(Chick$Time, Chick$weight)
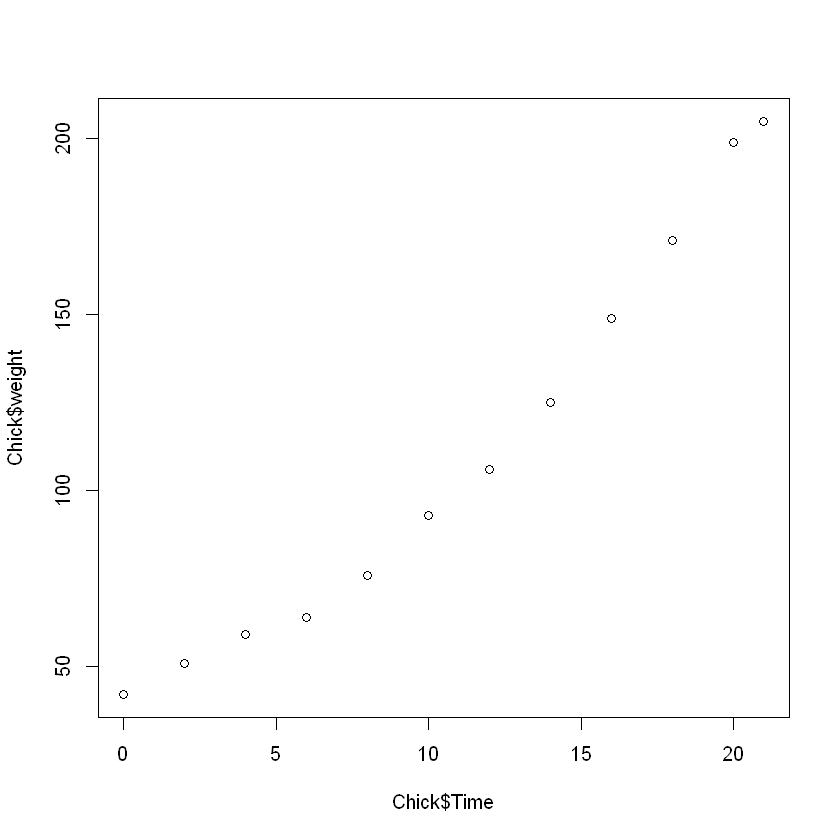
결과
추정된 회귀식
weight = 24.4654 + 7.9879*time
- F통계량:232.7 p-값:2.974e-08 –> 유의수준 5% 하에서 추정된 회귀 모형이 통계적으로 매우 유의함.
- 결정계수 또한 0.9588로 매우 노은 값을 보이므로 이 회귀식이 데이터를 96% 정도로 설명하고 있음.
- 회귀계수들의 p-값들도 0.05보다 매우 작으므로 회귀계수의 추정치들이 유의수준 5% 하에서 통계적으로 유의함.
해석
time이 1 증가할 때, weight이 7.99 만큼 증가한다.
다항회귀분석
dist = a + bspeed + cspeed^2 + e
data(cars)
print(head(cars))
speed dist
1 4 2
2 4 10
3 7 4
4 7 22
5 8 16
6 9 10
plot(cars$speed, cars$dist)
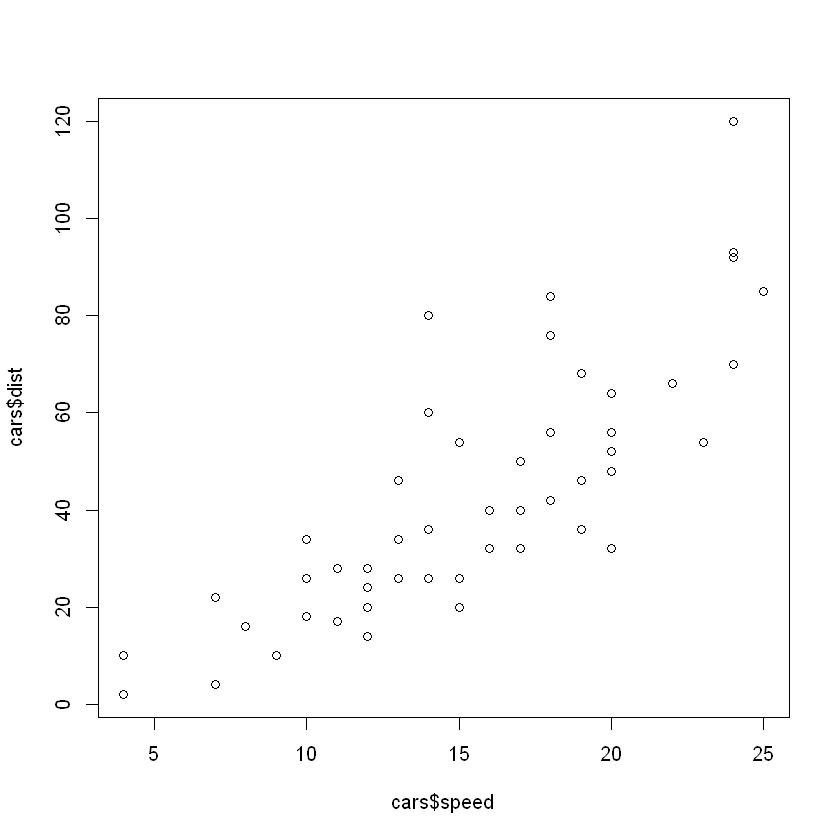
cars$speed2 = cars$speed^2
plot(cars$speed2, cars$dist)
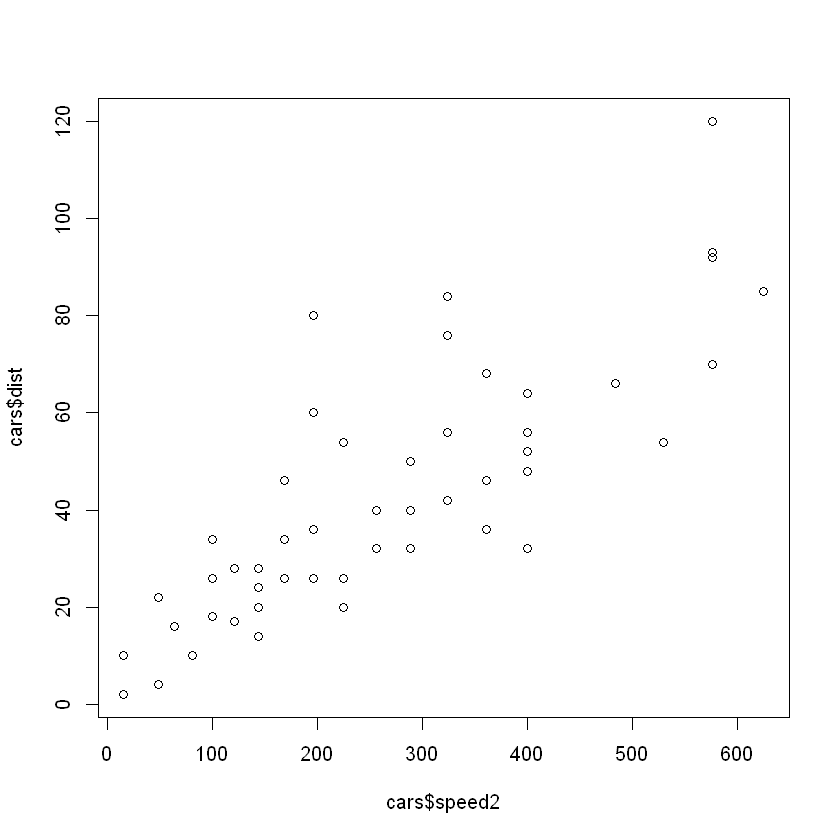
model = lm(cars$dist~speed+speed2, cars)
model
Call:
lm(formula = cars$dist ~ speed + speed2, data = cars)
Coefficients:
(Intercept) speed speed2
2.47014 0.91329 0.09996
summary(model)
Call:
lm(formula = cars$dist ~ speed + speed2, data = cars)
Residuals:
Min 1Q Median 3Q Max
-28.720 -9.184 -3.188 4.628 45.152
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.47014 14.81716 0.167 0.868
speed 0.91329 2.03422 0.449 0.656
speed2 0.09996 0.06597 1.515 0.136
Residual standard error: 15.18 on 47 degrees of freedom
Multiple R-squared: 0.6673, Adjusted R-squared: 0.6532
F-statistic: 47.14 on 2 and 47 DF, p-value: 5.852e-12
결과
추정된 회귀식
dist = 2.47014 + 0.91329speed + 0.09996speed^2
(예제) 적절한 회귀모형 탐색
## Data 생성
x=c(1:9)
y=c(5,3,2,3,4,6,10,12,18)
df=data.frame(x,y)
print(df)
x y
1 1 5
2 2 3
3 3 2
4 4 3
5 5 4
6 6 6
7 7 10
8 8 12
9 9 18
## EDA
plot(df$x, df$y) # 2차 함수 관계 파악
df$x2 = df$x^2 # x 제곱항 추가
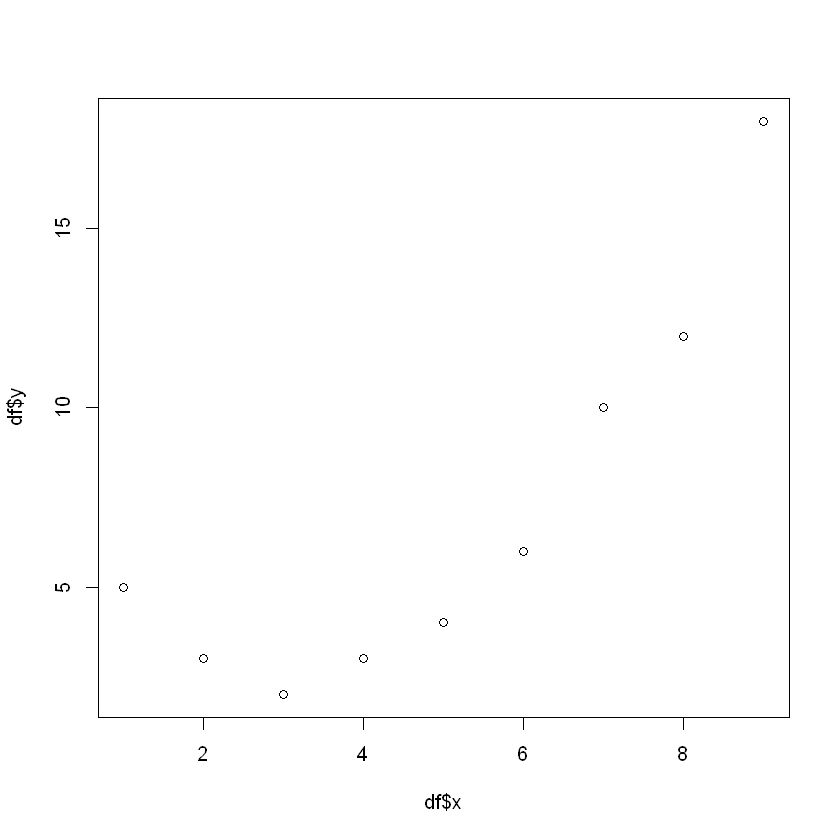
## 1) 제곱항 미포함 회귀식 적합
model1 = lm(y~x, df)
summary(model1)
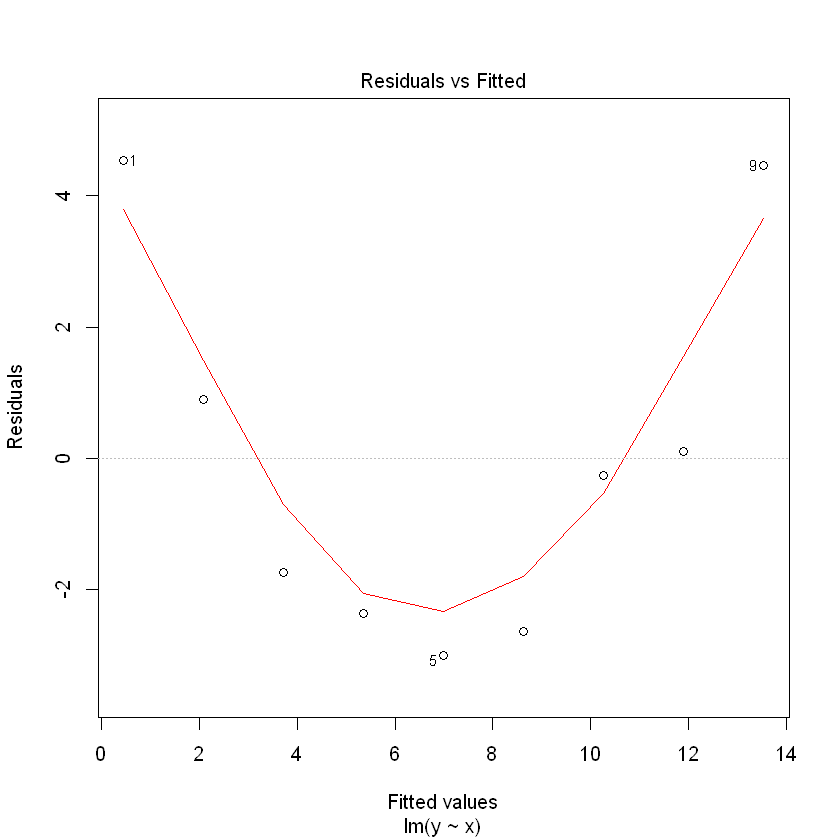
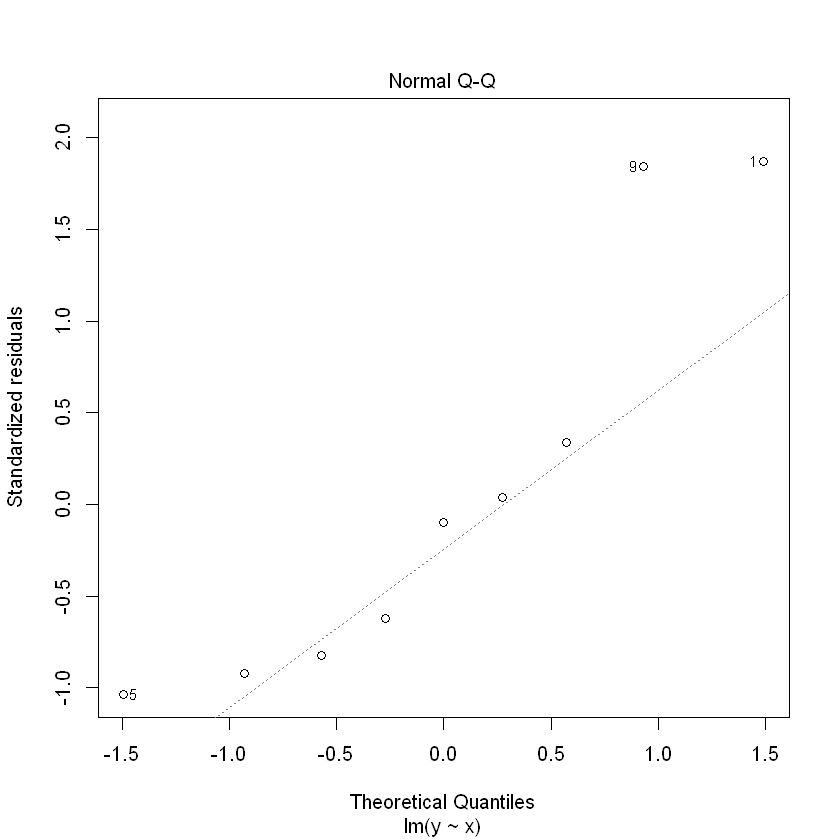
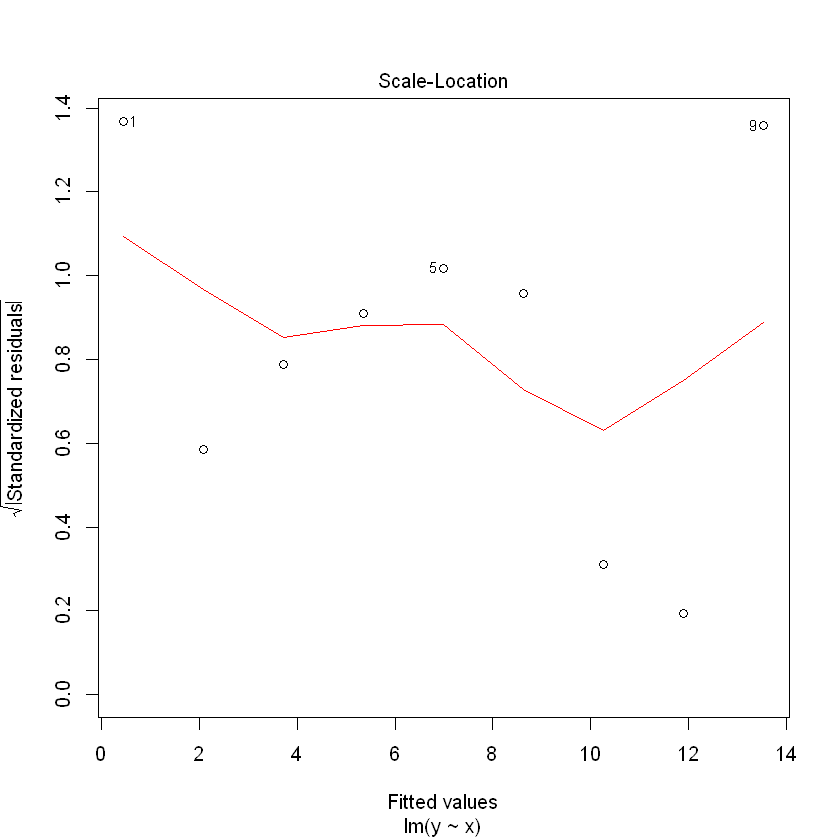
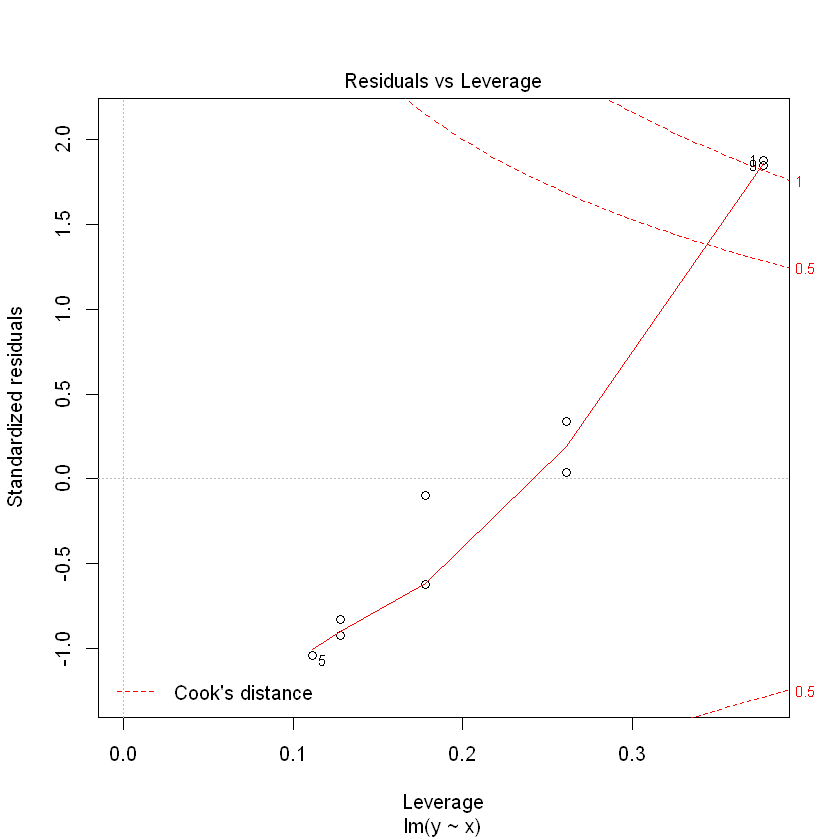
plot(model1)
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-3.0000 -2.3667 -0.2667 0.9000 4.5333
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -1.1667 2.2296 -0.523 0.61694
x 1.6333 0.3962 4.122 0.00445 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 3.069 on 7 degrees of freedom
Multiple R-squared: 0.7083, Adjusted R-squared: 0.6666
F-statistic: 16.99 on 1 and 7 DF, p-value: 0.004446
(추정된 회귀식)
y = -1.1667 + 1.6333*x
설명력 : 70.83%
(회귀식 잔차도 해석)
잔차가 곡선 패턴을 가지므로 오차팡은 평균이 0이고 분산이 일정하다는 가정을 만족하지 않음.
## 2) 제곱항 포함 회귀식 적합
model2 = lm(y~x+x2, df)
summary(model2)
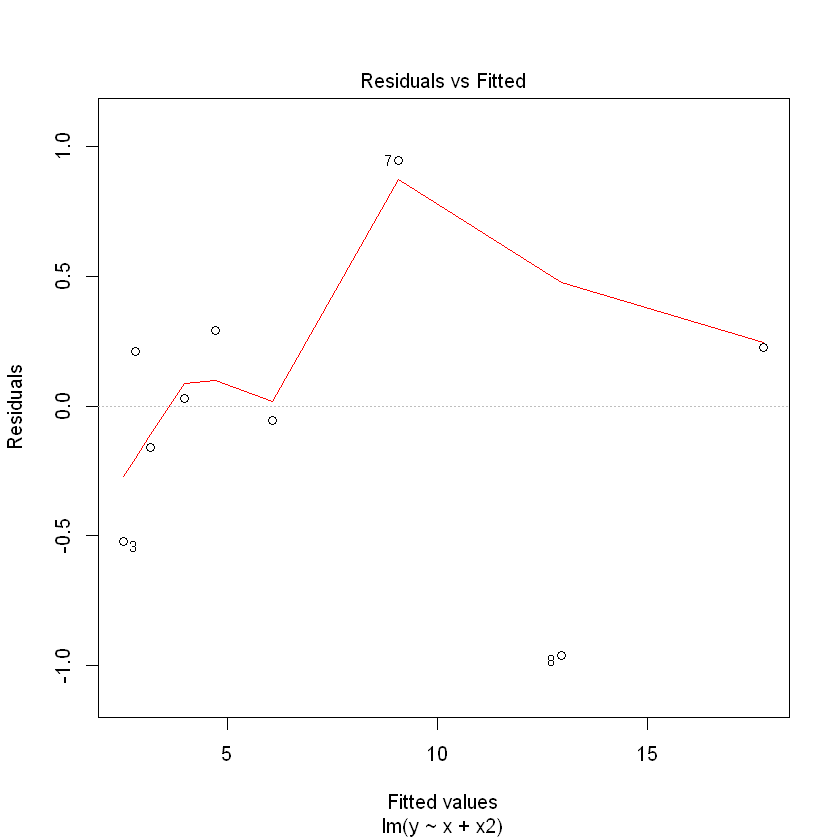
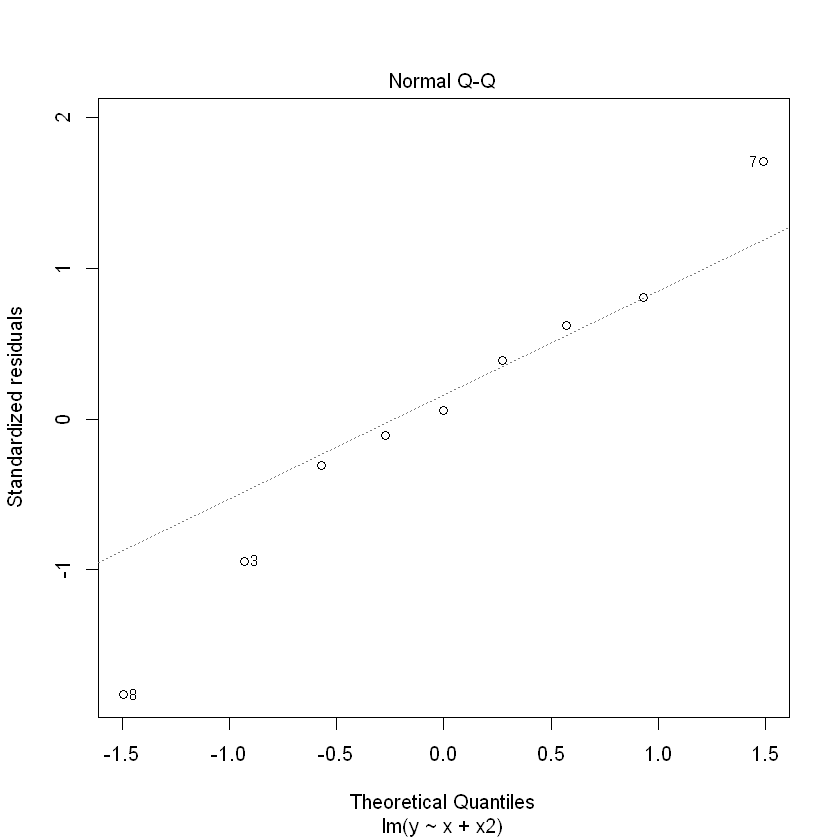
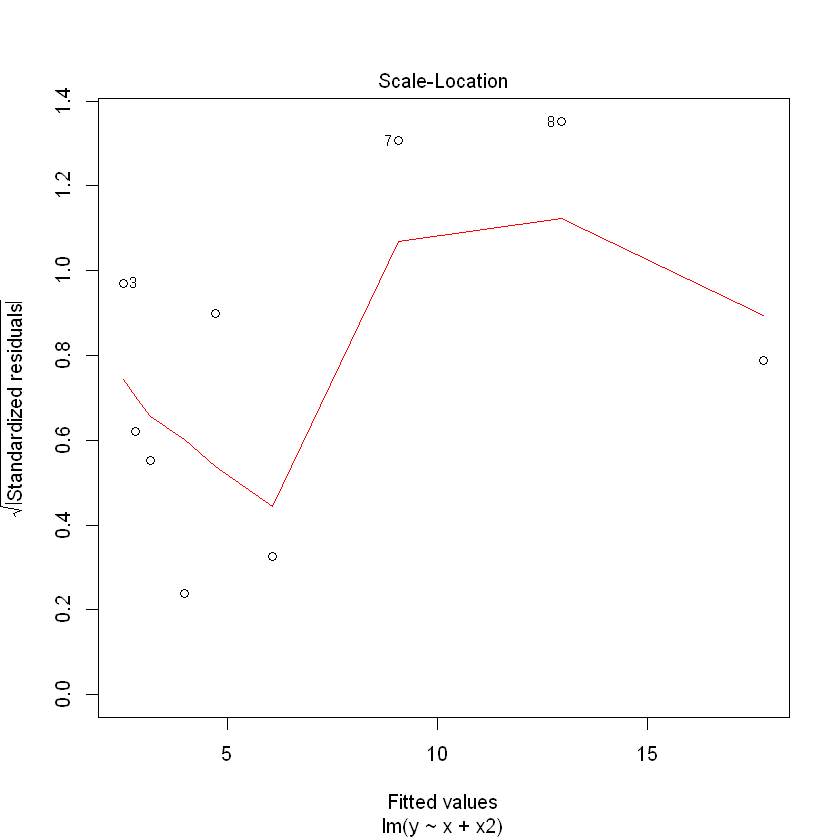
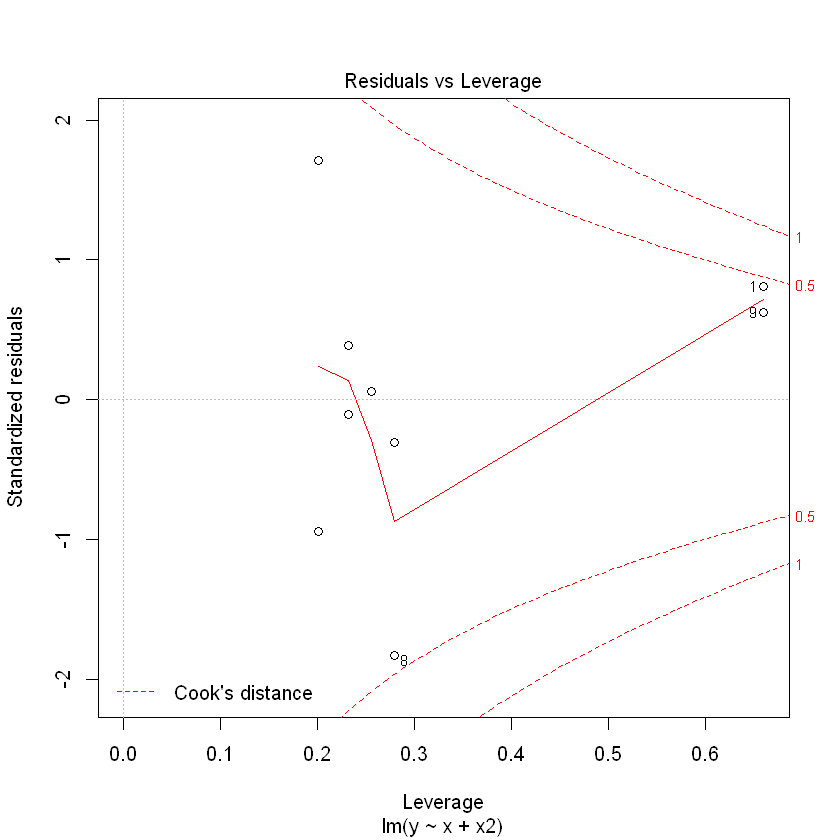
plot(model2)
Call:
lm(formula = y ~ x + x2, data = df)
Residuals:
Min 1Q Median 3Q Max
-0.9606 -0.1606 0.0303 0.2242 0.9455
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.16667 0.78728 9.103 9.87e-05 ***
x -2.91212 0.36149 -8.056 0.000196 ***
x2 0.45455 0.03526 12.893 1.34e-05 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.6187 on 6 degrees of freedom
Multiple R-squared: 0.9898, Adjusted R-squared: 0.9864
F-statistic: 292.2 on 2 and 6 DF, p-value: 1.05e-06
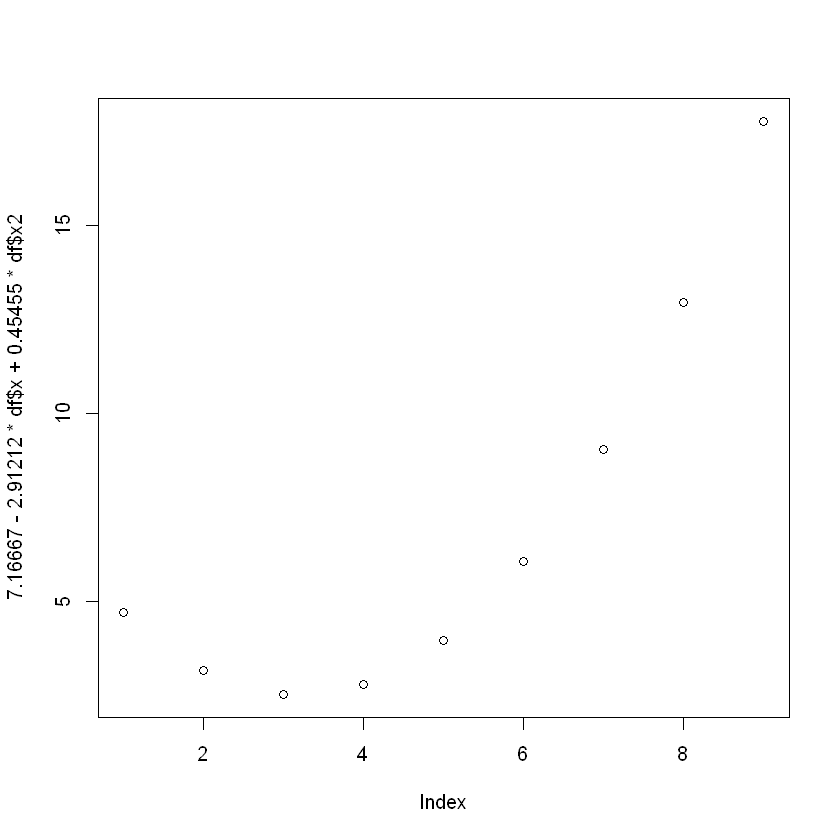
(추정된 회귀식)
y = 7.16667 - 2.91212x + 0.45455x^2
설명력 : 98.98%
(회귀식 잔차도 해석)
model1에 비해 다소 안정된 형태의 잔차를 보임.
plot(7.16667-2.91212*df$x+0.45455*df$x2)
plot(y)
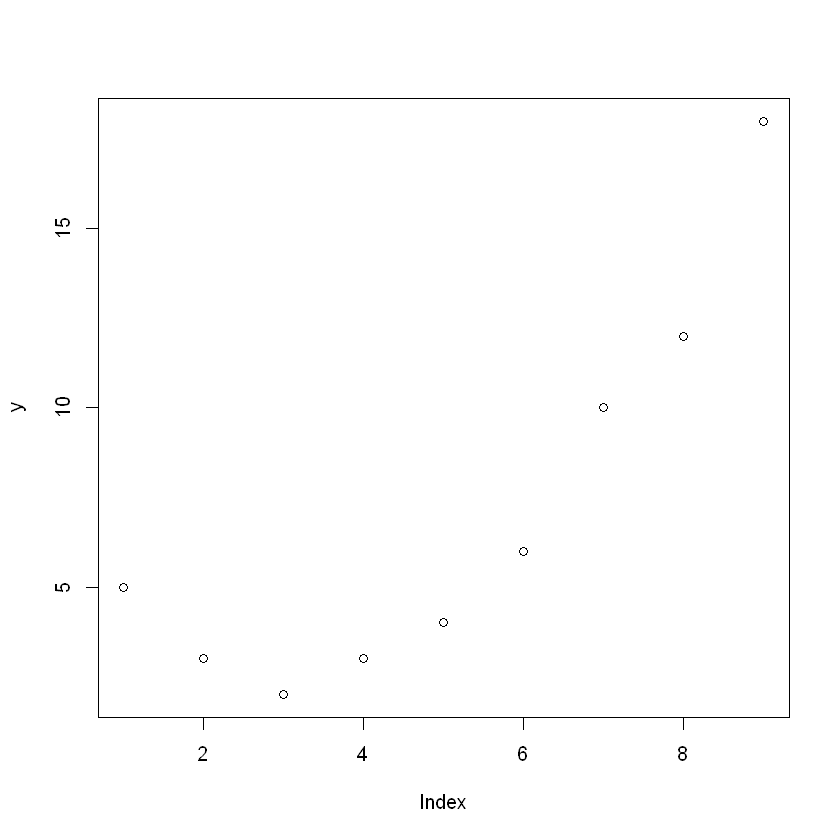
최적회귀방정식의 선택: 설명변수의 선택
(변수선택의 두 가지 원칙)
- y에 영향을 미칠 수 있는 모든 설명변수 x들을 y의 값을 예측하는데 참여시킨다.
- 데이터에 설명변수 x들의 수가 많아지면 관리하는데 많은 노력이 요구되므로,
가능한 범위 내에서 적은 수의 설명변수를 포함시켜야 한다.
- 위 두 가지 원칙은 서로 이율배반적이므로 타협이 이뤄져야 함.
즉, 상황에 적절한 설명변수를 선택해야 함.
1) 모든 가능한 조합의 회귀분석(All possible regression)
AIC(Akaike information criterion)
AIC = 2logL(theta hat) + 2*k
BIC(Bayesian information criterion)
BIC = 2logL(theta hat) + k*log(n)
–> n:자료의 갯수, theta hat:주어진 모형의 모수에 대한 최대가능도 추정량, L(theta hat):가능도함수, k:모형의 모수의 갯수
2) 단계적 변수선택(Stepwise Variable Selection)
- 전진선택법(forward selection)
절편만 있는 상수모형으로부터 시작해 중요하다고 생각되는 설명변수부터 차례로 모형에 추가함.
추가할 수 있는 후보가 되는 설명변수 중 모형에 추가했을 때 가장 제곱합의 기준으로 가장 설명을 잘하는 변수를 고려하여 그 변수가 유의하면 추가하고 그렇지 않은 경우는 추가를 멈춤.
- 후진선택법(backward selection)
독립변수 후보 모두를 포함한 모형에서 출발해 제곱합의 기준으로 가장 적은 영향을 주는 변수부터 하나씩 제거하면서 더 이상 유의하지 않은 변수가 없을 때까지 설명변수들을 제거하고, 이 때의 모형을 선택함.
- 단계별방법(stepwise method)
전진선택법에 의해 변수를 추가하면서 새롭게 추가된 변수에 기인해 기존 변수가 그 중요도가 약화되면 해당변수를 제거하는 등 단계별로 추가 또는 제거되는 변수의 여부를 검토해 더 이상 없을 때 중단함.
(예제) 선형회귀모형 설정 및 후진제거법 통한 변수선택
X1 = c(7,1,11,11,7,11,3,1,2,21,1,11,10)
X2 = c(26,29,56,31,52,55,71,31,54,47,40,66,68)
X3 = c(6,15,8,8,6,9,17,22,18,4,23,9,8)
X4 = c(60,52,20,47,33,22,6,44,22,26,34,12,12)
Y = c(78.5,74.3,104.3,87.6,95.9,109.2,102.7,72.5,93.1,115.9,83.8,113.3,109.4)
df = data.frame(X1,X2,X3,X4,Y)
print(df)
X1 X2 X3 X4 Y
1 7 26 6 60 78.5
2 1 29 15 52 74.3
3 11 56 8 20 104.3
4 11 31 8 47 87.6
5 7 52 6 33 95.9
6 11 55 9 22 109.2
7 3 71 17 6 102.7
8 1 31 22 44 72.5
9 2 54 18 22 93.1
10 21 47 4 26 115.9
11 1 40 23 34 83.8
12 11 66 9 12 113.3
13 10 68 8 12 109.4
model1 = lm(Y~X1+X2+X3+X4, df)
summary(model1) # X3 의 유의확률이 가장 높으므로 제거
Call:
lm(formula = Y ~ X1 + X2 + X3 + X4, data = df)
Residuals:
Min 1Q Median 3Q Max
-3.1750 -1.6709 0.2508 1.3783 3.9254
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 62.4054 70.0710 0.891 0.3991
X1 1.5511 0.7448 2.083 0.0708 .
X2 0.5102 0.7238 0.705 0.5009
X3 0.1019 0.7547 0.135 0.8959
X4 -0.1441 0.7091 -0.203 0.8441
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.446 on 8 degrees of freedom
Multiple R-squared: 0.9824, Adjusted R-squared: 0.9736
F-statistic: 111.5 on 4 and 8 DF, p-value: 4.756e-07
model2 = lm(Y~X1+X2+X4, df)
summary(model2) # X4 의 유의확률이 가장 높으므로 제거
Call:
lm(formula = Y ~ X1 + X2 + X4, data = df)
Residuals:
Min 1Q Median 3Q Max
-3.0919 -1.8016 0.2562 1.2818 3.8982
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 71.6483 14.1424 5.066 0.000675 ***
X1 1.4519 0.1170 12.410 5.78e-07 ***
X2 0.4161 0.1856 2.242 0.051687 .
X4 -0.2365 0.1733 -1.365 0.205395
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.309 on 9 degrees of freedom
Multiple R-squared: 0.9823, Adjusted R-squared: 0.9764
F-statistic: 166.8 on 3 and 9 DF, p-value: 3.323e-08
model3 = lm(Y~X1+X2, df)
summary(model3)
Call:
lm(formula = Y ~ X1 + X2, data = df)
Residuals:
Min 1Q Median 3Q Max
-2.893 -1.574 -1.302 1.363 4.048
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 52.57735 2.28617 23.00 5.46e-10 ***
X1 1.46831 0.12130 12.11 2.69e-07 ***
X2 0.66225 0.04585 14.44 5.03e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.406 on 10 degrees of freedom
Multiple R-squared: 0.9787, Adjusted R-squared: 0.9744
F-statistic: 229.5 on 2 and 10 DF, p-value: 4.407e-09
위 과정의 후진제거법을 자동으로 실행
step(lm(종속변수~설명변수, 데이터세트), scope=list(lower=~1, upper=~설명변수), direction=”변수선택방법”)
# 후진제거법
step(lm(Y~X1+X2+X3+X4, df), scope=list(lower=~1, upper=~X1+X2+X3+X4), direction = "backward")
Start: AIC=26.94
Y ~ X1 + X2 + X3 + X4
Df Sum of Sq RSS AIC
- X3 1 0.1091 47.973 24.974
- X4 1 0.2470 48.111 25.011
- X2 1 2.9725 50.836 25.728
<none> 47.864 26.944
- X1 1 25.9509 73.815 30.576
Step: AIC=24.97
Y ~ X1 + X2 + X4
Df Sum of Sq RSS AIC
<none> 47.97 24.974
- X4 1 9.93 57.90 25.420
- X2 1 26.79 74.76 28.742
- X1 1 820.91 868.88 60.629
Call:
lm(formula = Y ~ X1 + X2 + X4, data = df)
Coefficients:
(Intercept) X1 X2 X4
71.6483 1.4519 0.4161 -0.2365
# 전진선택법
step(lm(Y~1, df), scope=list(lower=~1, upper=~X1+X2+X3+X4), direction = "forward")
Start: AIC=71.44
Y ~ 1
Df Sum of Sq RSS AIC
+ X4 1 1831.90 883.87 58.852
+ X2 1 1809.43 906.34 59.178
+ X1 1 1450.08 1265.69 63.519
+ X3 1 776.36 1939.40 69.067
<none> 2715.76 71.444
Step: AIC=58.85
Y ~ X4
Df Sum of Sq RSS AIC
+ X1 1 809.10 74.76 28.742
+ X3 1 708.13 175.74 39.853
<none> 883.87 58.852
+ X2 1 14.99 868.88 60.629
Step: AIC=28.74
Y ~ X4 + X1
Df Sum of Sq RSS AIC
+ X2 1 26.789 47.973 24.974
+ X3 1 23.926 50.836 25.728
<none> 74.762 28.742
Step: AIC=24.97
Y ~ X4 + X1 + X2
Df Sum of Sq RSS AIC
<none> 47.973 24.974
+ X3 1 0.10909 47.864 26.944
Call:
lm(formula = Y ~ X4 + X1 + X2, data = df)
Coefficients:
(Intercept) X4 X1 X2
71.6483 -0.2365 1.4519 0.4161
# 단계선택법
step(lm(Y~1, df), scope=list(lower=~1, upper=~X1+X2+X3+X4), direction = "both")
Start: AIC=71.44
Y ~ 1
Df Sum of Sq RSS AIC
+ X4 1 1831.90 883.87 58.852
+ X2 1 1809.43 906.34 59.178
+ X1 1 1450.08 1265.69 63.519
+ X3 1 776.36 1939.40 69.067
<none> 2715.76 71.444
Step: AIC=58.85
Y ~ X4
Df Sum of Sq RSS AIC
+ X1 1 809.10 74.76 28.742
+ X3 1 708.13 175.74 39.853
<none> 883.87 58.852
+ X2 1 14.99 868.88 60.629
- X4 1 1831.90 2715.76 71.444
Step: AIC=28.74
Y ~ X4 + X1
Df Sum of Sq RSS AIC
+ X2 1 26.79 47.97 24.974
+ X3 1 23.93 50.84 25.728
<none> 74.76 28.742
- X1 1 809.10 883.87 58.852
- X4 1 1190.92 1265.69 63.519
Step: AIC=24.97
Y ~ X4 + X1 + X2
Df Sum of Sq RSS AIC
<none> 47.97 24.974
- X4 1 9.93 57.90 25.420
+ X3 1 0.11 47.86 26.944
- X2 1 26.79 74.76 28.742
- X1 1 820.91 868.88 60.629
Call:
lm(formula = Y ~ X4 + X1 + X2, data = df)
Coefficients:
(Intercept) X4 X1 X2
71.6483 -0.2365 1.4519 0.4161
# 적용
library(MASS)
data(hills)
print(head(hills))
dist climb time
Greenmantle 2.5 650 16.083
Carnethy 6.0 2500 48.350
Craig Dunain 6.0 900 33.650
Ben Rha 7.5 800 45.600
Ben Lomond 8.0 3070 62.267
Goatfell 8.0 2866 73.217
model = step(lm(time~1, hills), scope = list(lower=~1, upper=~dist+climb), direction = 'both')
summary(model)
Start: AIC=274.88
time ~ 1
Df Sum of Sq RSS AIC
+ dist 1 71997 13142 211.49
+ climb 1 55205 29934 240.30
<none> 85138 274.88
Step: AIC=211.49
time ~ dist
Df Sum of Sq RSS AIC
+ climb 1 6250 6892 190.90
<none> 13142 211.49
- dist 1 71997 85138 274.88
Step: AIC=190.9
time ~ dist + climb
Df Sum of Sq RSS AIC
<none> 6891.9 190.90
- climb 1 6249.7 13141.6 211.49
- dist 1 23042.0 29933.8 240.30
Call:
lm(formula = time ~ dist + climb, data = hills)
Residuals:
Min 1Q Median 3Q Max
-16.215 -7.129 -1.186 2.371 65.121
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -8.992039 4.302734 -2.090 0.0447 *
dist 6.217956 0.601148 10.343 9.86e-12 ***
climb 0.011048 0.002051 5.387 6.45e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 14.68 on 32 degrees of freedom
Multiple R-squared: 0.9191, Adjusted R-squared: 0.914
F-statistic: 181.7 on 2 and 32 DF, p-value: < 2.2e-16
댓글남기기