제2장 : 통계 분석
먼저 데이터 분석을 수행할 환경의 경로를 설정합니다.
# Working Directory
setwd('C:/Users/wooil/Documents/GitHub/ADP')
getwd()
‘C:/Users/wooil/Documents/GitHub/ADP’
제3절 다변량 분석
1. 상관 분석
피어슨의 상관계수
# (예제)
install.packages("Hmisc")
library(Hmisc)
Installing package into 'C:/Users/wooil/Documents/R/win-library/3.6'
(as 'lib' is unspecified)
package 'Hmisc' successfully unpacked and MD5 sums checked
The downloaded binary packages are in
C:\Users\wooil\AppData\Local\Temp\RtmpoVx66K\downloaded_packages
Loading required package: lattice
Loading required package: survival
Loading required package: Formula
Loading required package: ggplot2
Registered S3 methods overwritten by 'ggplot2':
method from
[.quosures rlang
c.quosures rlang
print.quosures rlang
Attaching package: 'Hmisc'
The following objects are masked from 'package:base':
format.pval, units
data(mtcars)
print(head(mtcars))
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3.460 20.22 1 0 3 1
mtcars 데이터셋의 drat, disp 간 산점도와 상관계수
plot(mtcars$drat, mtcars$disp) # 음의 직선관계 존재 확인
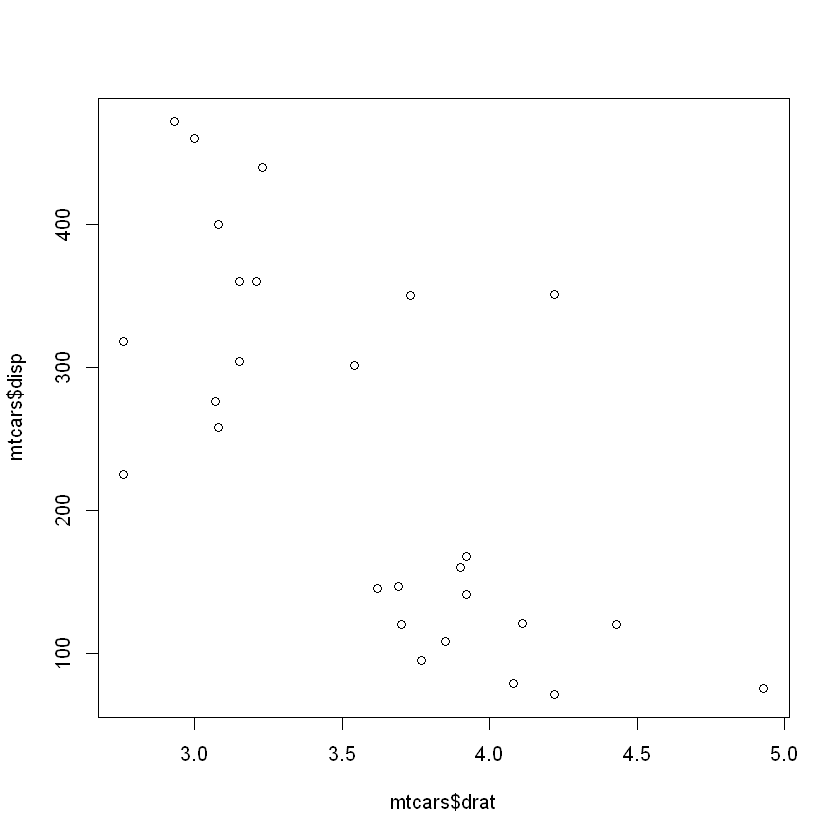
cor(mtcars$drat, mtcars$disp) # 상관계수 : -0.71
-0.71021392716927
# mtcars 모든 변수 간 상관계수 - 'rcorr' 함수 이용
rcorr(as.matrix(mtcars), type='pearson') # 상관계수 행렬과 P-Value 행렬 출력('carb'와 'am' p-value > 0.05 이므로 유의하지 않음)
mpg cyl disp hp drat wt qsec vs am gear carb
mpg 1.00 -0.85 -0.85 -0.78 0.68 -0.87 0.42 0.66 0.60 0.48 -0.55
cyl -0.85 1.00 0.90 0.83 -0.70 0.78 -0.59 -0.81 -0.52 -0.49 0.53
disp -0.85 0.90 1.00 0.79 -0.71 0.89 -0.43 -0.71 -0.59 -0.56 0.39
hp -0.78 0.83 0.79 1.00 -0.45 0.66 -0.71 -0.72 -0.24 -0.13 0.75
drat 0.68 -0.70 -0.71 -0.45 1.00 -0.71 0.09 0.44 0.71 0.70 -0.09
wt -0.87 0.78 0.89 0.66 -0.71 1.00 -0.17 -0.55 -0.69 -0.58 0.43
qsec 0.42 -0.59 -0.43 -0.71 0.09 -0.17 1.00 0.74 -0.23 -0.21 -0.66
vs 0.66 -0.81 -0.71 -0.72 0.44 -0.55 0.74 1.00 0.17 0.21 -0.57
am 0.60 -0.52 -0.59 -0.24 0.71 -0.69 -0.23 0.17 1.00 0.79 0.06
gear 0.48 -0.49 -0.56 -0.13 0.70 -0.58 -0.21 0.21 0.79 1.00 0.27
carb -0.55 0.53 0.39 0.75 -0.09 0.43 -0.66 -0.57 0.06 0.27 1.00
n= 32
P
mpg cyl disp hp drat wt qsec vs am gear
mpg 0.0000 0.0000 0.0000 0.0000 0.0000 0.0171 0.0000 0.0003 0.0054
cyl 0.0000 0.0000 0.0000 0.0000 0.0000 0.0004 0.0000 0.0022 0.0042
disp 0.0000 0.0000 0.0000 0.0000 0.0000 0.0131 0.0000 0.0004 0.0010
hp 0.0000 0.0000 0.0000 0.0100 0.0000 0.0000 0.0000 0.1798 0.4930
drat 0.0000 0.0000 0.0000 0.0100 0.0000 0.6196 0.0117 0.0000 0.0000
wt 0.0000 0.0000 0.0000 0.0000 0.0000 0.3389 0.0010 0.0000 0.0005
qsec 0.0171 0.0004 0.0131 0.0000 0.6196 0.3389 0.0000 0.2057 0.2425
vs 0.0000 0.0000 0.0000 0.0000 0.0117 0.0010 0.0000 0.3570 0.2579
am 0.0003 0.0022 0.0004 0.1798 0.0000 0.0000 0.2057 0.3570 0.0000
gear 0.0054 0.0042 0.0010 0.4930 0.0000 0.0005 0.2425 0.2579 0.0000
carb 0.0011 0.0019 0.0253 0.0000 0.6212 0.0146 0.0000 0.0007 0.7545 0.1290
carb
mpg 0.0011
cyl 0.0019
disp 0.0253
hp 0.0000
drat 0.6212
wt 0.0146
qsec 0.0000
vs 0.0007
am 0.7545
gear 0.1290
carb
# 공분산(Covariance) 출력
print(cov(mtcars))
mpg cyl disp hp drat wt
mpg 36.324103 -9.1723790 -633.09721 -320.732056 2.19506351 -5.1166847
cyl -9.172379 3.1895161 199.66028 101.931452 -0.66836694 1.3673710
disp -633.097208 199.6602823 15360.79983 6721.158669 -47.06401915 107.6842040
hp -320.732056 101.9314516 6721.15867 4700.866935 -16.45110887 44.1926613
drat 2.195064 -0.6683669 -47.06402 -16.451109 0.28588135 -0.3727207
wt -5.116685 1.3673710 107.68420 44.192661 -0.37272073 0.9573790
qsec 4.509149 -1.8868548 -96.05168 -86.770081 0.08714073 -0.3054816
vs 2.017137 -0.7298387 -44.37762 -24.987903 0.11864919 -0.2736613
am 1.803931 -0.4657258 -36.56401 -8.320565 0.19015121 -0.3381048
gear 2.135685 -0.6491935 -50.80262 -6.358871 0.27598790 -0.4210806
carb -5.363105 1.5201613 79.06875 83.036290 -0.07840726 0.6757903
qsec vs am gear carb
mpg 4.50914919 2.01713710 1.80393145 2.1356855 -5.36310484
cyl -1.88685484 -0.72983871 -0.46572581 -0.6491935 1.52016129
disp -96.05168145 -44.37762097 -36.56401210 -50.8026210 79.06875000
hp -86.77008065 -24.98790323 -8.32056452 -6.3588710 83.03629032
drat 0.08714073 0.11864919 0.19015121 0.2759879 -0.07840726
wt -0.30548161 -0.27366129 -0.33810484 -0.4210806 0.67579032
qsec 3.19316613 0.67056452 -0.20495968 -0.2804032 -1.89411290
vs 0.67056452 0.25403226 0.04233871 0.0766129 -0.46370968
am -0.20495968 0.04233871 0.24899194 0.2923387 0.04637097
gear -0.28040323 0.07661290 0.29233871 0.5443548 0.32661290
carb -1.89411290 -0.46370968 0.04637097 0.3266129 2.60887097
스피어만의 상관계수(Spearman’s rank correlation coefficient)
피어슨의 상관계수는 두 변수 간의 선형관계의 크기를 측정하는 값으로 비선형적인 상관관계는 나타내지 못함.
스피어만 상관계수는 두 변수 간의 비선형적인 관계도 나타낼 수 있는 값으로, 한 변수를 단조 증가 함수로 변환하여 다른 변수를 나타낼 수 있는 정도를 나타냄.
스피어만의 상관계수는 두 변수를 모두 순위로 변환시킨 후, 두 순위 사이의 피어슨 상관계수로 정의 됨.
스피어만 상관계수 행렬 출력
rcorr(as.matrix(mtcars), type="spearman")
mpg cyl disp hp drat wt qsec vs am gear carb
mpg 1.00 -0.91 -0.91 -0.89 0.65 -0.89 0.47 0.71 0.56 0.54 -0.66
cyl -0.91 1.00 0.93 0.90 -0.68 0.86 -0.57 -0.81 -0.52 -0.56 0.58
disp -0.91 0.93 1.00 0.85 -0.68 0.90 -0.46 -0.72 -0.62 -0.59 0.54
hp -0.89 0.90 0.85 1.00 -0.52 0.77 -0.67 -0.75 -0.36 -0.33 0.73
drat 0.65 -0.68 -0.68 -0.52 1.00 -0.75 0.09 0.45 0.69 0.74 -0.13
wt -0.89 0.86 0.90 0.77 -0.75 1.00 -0.23 -0.59 -0.74 -0.68 0.50
qsec 0.47 -0.57 -0.46 -0.67 0.09 -0.23 1.00 0.79 -0.20 -0.15 -0.66
vs 0.71 -0.81 -0.72 -0.75 0.45 -0.59 0.79 1.00 0.17 0.28 -0.63
am 0.56 -0.52 -0.62 -0.36 0.69 -0.74 -0.20 0.17 1.00 0.81 -0.06
gear 0.54 -0.56 -0.59 -0.33 0.74 -0.68 -0.15 0.28 0.81 1.00 0.11
carb -0.66 0.58 0.54 0.73 -0.13 0.50 -0.66 -0.63 -0.06 0.11 1.00
n= 32
P
mpg cyl disp hp drat wt qsec vs am gear
mpg 0.0000 0.0000 0.0000 0.0000 0.0000 0.0071 0.0000 0.0008 0.0013
cyl 0.0000 0.0000 0.0000 0.0000 0.0000 0.0006 0.0000 0.0022 0.0008
disp 0.0000 0.0000 0.0000 0.0000 0.0000 0.0081 0.0000 0.0001 0.0003
hp 0.0000 0.0000 0.0000 0.0023 0.0000 0.0000 0.0000 0.0416 0.0639
drat 0.0000 0.0000 0.0000 0.0023 0.0000 0.6170 0.0102 0.0000 0.0000
wt 0.0000 0.0000 0.0000 0.0000 0.0000 0.2148 0.0004 0.0000 0.0000
qsec 0.0071 0.0006 0.0081 0.0000 0.6170 0.2148 0.0000 0.2644 0.4182
vs 0.0000 0.0000 0.0000 0.0000 0.0102 0.0004 0.0000 0.3570 0.1170
am 0.0008 0.0022 0.0001 0.0416 0.0000 0.0000 0.2644 0.3570 0.0000
gear 0.0013 0.0008 0.0003 0.0639 0.0000 0.0000 0.4182 0.1170 0.0000
carb 0.0000 0.0005 0.0014 0.0000 0.4947 0.0036 0.0000 0.0000 0.7264 0.5312
carb
mpg 0.0000
cyl 0.0005
disp 0.0014
hp 0.0000
drat 0.4947
wt 0.0036
qsec 0.0000
vs 0.0000
am 0.7264
gear 0.5312
carb
2. 다차원 척도법(Multidimensional Scaling, MDS)
다차원척도법은 여러 대상 간의 거리가 주어져 있을 때, 대상들을 동일한 상대적 거리를 가진 실수공간의 점들로 배치시키는 방법을 말함.
주어진 거리는 추상적인 대상들 간의 거리가 될 수도 있고, 실수공간에서의 거리가 될 수도 있음.
대상들을 2차원이나 3차원 실수공간의 점으로 대응시킬 수 있다면 이 점들을 시각화할 수 있고, 이는 관측치들 간의 전반적 관계에 대한 직관적 이해를 할 수 있게 도와줌. 따라서 다차원척도법은 주로 자료들의 상대적 관계를 이해하는 시각화 방법의 근간으로 주로 사용됨.
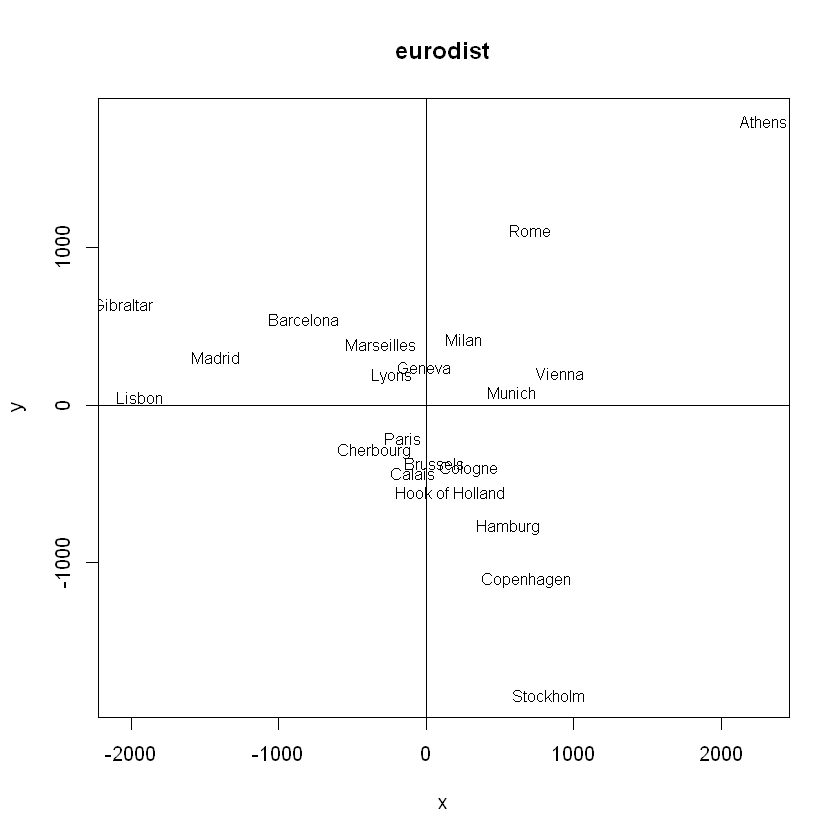
(예제) euridist 데이터 - 도시 사이의 거리 매핑
data(eurodist)
print(eurodist)
Athens Barcelona Brussels Calais Cherbourg Cologne Copenhagen
Barcelona 3313
Brussels 2963 1318
Calais 3175 1326 204
Cherbourg 3339 1294 583 460
Cologne 2762 1498 206 409 785
Copenhagen 3276 2218 966 1136 1545 760
Geneva 2610 803 677 747 853 1662 1418
Gibraltar 4485 1172 2256 2224 2047 2436 3196
Hamburg 2977 2018 597 714 1115 460 460
Hook of Holland 3030 1490 172 330 731 269 269
Lisbon 4532 1305 2084 2052 1827 2290 2971
Lyons 2753 645 690 739 789 714 1458
Madrid 3949 636 1558 1550 1347 1764 2498
Marseilles 2865 521 1011 1059 1101 1035 1778
Milan 2282 1014 925 1077 1209 911 1537
Munich 2179 1365 747 977 1160 583 1104
Paris 3000 1033 285 280 340 465 1176
Rome 817 1460 1511 1662 1794 1497 2050
Stockholm 3927 2868 1616 1786 2196 1403 650
Vienna 1991 1802 1175 1381 1588 937 1455
Geneva Gibraltar Hamburg Hook of Holland Lisbon Lyons Madrid
Barcelona
Brussels
Calais
Cherbourg
Cologne
Copenhagen
Geneva
Gibraltar 1975
Hamburg 1118 2897
Hook of Holland 895 2428 550
Lisbon 1936 676 2671 2280
Lyons 158 1817 1159 863 1178
Madrid 1439 698 2198 1730 668 1281
Marseilles 425 1693 1479 1183 1762 320 1157
Milan 328 2185 1238 1098 2250 328 1724
Munich 591 2565 805 851 2507 724 2010
Paris 513 1971 877 457 1799 471 1273
Rome 995 2631 1751 1683 2700 1048 2097
Stockholm 2068 3886 949 1500 3231 2108 3188
Vienna 1019 2974 1155 1205 2937 1157 2409
Marseilles Milan Munich Paris Rome Stockholm
Barcelona
Brussels
Calais
Cherbourg
Cologne
Copenhagen
Geneva
Gibraltar
Hamburg
Hook of Holland
Lisbon
Lyons
Madrid
Marseilles
Milan 618
Munich 1109 331
Paris 792 856 821
Rome 1011 586 946 1476
Stockholm 2428 2187 1754 1827 2707
Vienna 1363 898 428 1249 1209 2105
loc = cmdscale(eurodist)
print(loc)
[,1] [,2]
Athens 2290.274680 1798.80293
Barcelona -825.382790 546.81148
Brussels 59.183341 -367.08135
Calais -82.845973 -429.91466
Cherbourg -352.499435 -290.90843
Cologne 293.689633 -405.31194
Copenhagen 681.931545 -1108.64478
Geneva -9.423364 240.40600
Gibraltar -2048.449113 642.45854
Hamburg 561.108970 -773.36929
Hook of Holland 164.921799 -549.36704
Lisbon -1935.040811 49.12514
Lyons -226.423236 187.08779
Madrid -1423.353697 305.87513
Marseilles -299.498710 388.80726
Milan 260.878046 416.67381
Munich 587.675679 81.18224
Paris -156.836257 -211.13911
Rome 709.413282 1109.36665
Stockholm 839.445911 -1836.79055
Vienna 911.230500 205.93020
x = loc[, 1]
y = loc[, 2]
plot(x,y, type='n', main='eurodist')
text(x,y,rownames(loc),cex=0.8)
abline(v=0, h=0)
3. 주성분 분석(Principal Component Analysis)
주성분 분석은 상관관계가 있는 고차원 자료를 자료의 변동을 최대한 보존하는 저차원 자료로 변환시키는 방법으로, 자료의 차원을 축약시키는데 주로 활용됨.
정의에 따라 주성분들은 서로 상관관계가 없고, 주성분들의 분산의 합은 Xi들의 분산의 합과 같음.
# (예제) 미국 50개 주 인구 10만명 당 살인, 폭행, 강간으로 인한 체포의 수와 도시 인구의 비율
library(datasets)
data(USArrests)
print(head(USArrests))
summary(USArrests)
Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7
Murder Assault UrbanPop Rape
Min. : 0.800 Min. : 45.0 Min. :32.00 Min. : 7.30
1st Qu.: 4.075 1st Qu.:109.0 1st Qu.:54.50 1st Qu.:15.07
Median : 7.250 Median :159.0 Median :66.00 Median :20.10
Mean : 7.788 Mean :170.8 Mean :65.54 Mean :21.23
3rd Qu.:11.250 3rd Qu.:249.0 3rd Qu.:77.75 3rd Qu.:26.18
Max. :17.400 Max. :337.0 Max. :91.00 Max. :46.00
주성분 분석 - cor=TRUE : 공분산 행렬이 아닌 상관계수 행렬 사용하여 수행
fit = princomp(USArrests, cor=TRUE)
주성분의 표준편차, 분산의 비율 등 출력 : 주성분1이 총 분산의 62% 설명
summary(fit)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4
Standard deviation 1.5748783 0.9948694 0.5971291 0.41644938
Proportion of Variance 0.6200604 0.2474413 0.0891408 0.04335752
Cumulative Proportion 0.6200604 0.8675017 0.9566425 1.00000000
주성분들의 로딩 벡터 출력
loadings(fit)
Loadings:
Comp.1 Comp.2 Comp.3 Comp.4
Murder 0.536 0.418 0.341 0.649
Assault 0.583 0.188 0.268 -0.743
UrbanPop 0.278 -0.873 0.378 0.134
Rape 0.543 -0.167 -0.818
Comp.1 Comp.2 Comp.3 Comp.4
SS loadings 1.00 1.00 1.00 1.00
Proportion Var 0.25 0.25 0.25 0.25
Cumulative Var 0.25 0.50 0.75 1.00
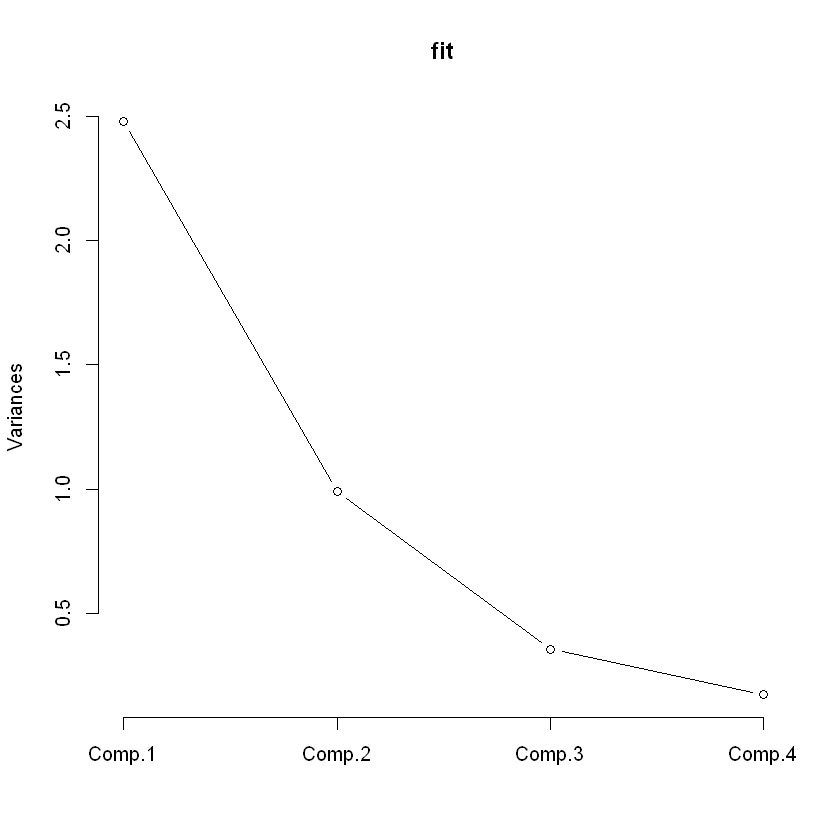
각 주성분의 분산의 크기를 출력 : 스크리 플롯(Scree plot)
주성분의 분산의 감소가 급격하게 줄어들어 주성분의 갯수를 늘릴 때 얻게되는 정보의 양이 상대적으로 미미한 지점에서 주성분의 갯수를 정하는 것이 하나의 방법임.
그 외에도 주성분들이 설명하는 총 분산의 비율이 70~90% 사이가 되는 주성분의 갯수를 선택하는 방법을 사용하기도 함.
plot(fit, type='lines')
각 관측치를 주성분들로 표현한 값 출력
print(fit$scores)
Comp.1 Comp.2 Comp.3 Comp.4
Alabama 0.98556588 1.13339238 0.44426879 0.156267145
Alaska 1.95013775 1.07321326 -2.04000333 -0.438583440
Arizona 1.76316354 -0.74595678 -0.05478082 -0.834652924
Arkansas -0.14142029 1.11979678 -0.11457369 -0.182810896
California 2.52398013 -1.54293399 -0.59855680 -0.341996478
Colorado 1.51456286 -0.98755509 -1.09500699 0.001464887
Connecticut -1.35864746 -1.08892789 0.64325757 -0.118469414
Delaware 0.04770931 -0.32535892 0.71863294 -0.881977637
Florida 3.01304227 0.03922851 0.57682949 -0.096284752
Georgia 1.63928304 1.27894240 0.34246008 1.076796812
Hawaii -0.91265715 -1.57046001 -0.05078189 0.902806864
Idaho -1.63979985 0.21097292 -0.25980134 -0.499104101
Illinois 1.37891072 -0.68184119 0.67749564 -0.122021292
Indiana -0.50546136 -0.15156254 -0.22805484 0.424665700
Iowa -2.25364607 -0.10405407 -0.16456432 0.017555916
Kansas -0.79688112 -0.27016470 -0.02555331 0.206496428
Kentucky -0.75085907 0.95844029 0.02836942 0.670556671
Louisiana 1.56481798 0.87105466 0.78348036 0.454728038
Maine -2.39682949 0.37639158 0.06568239 -0.330459817
Maryland 1.76336939 0.42765519 0.15725013 -0.559069521
Massachusetts -0.48616629 -1.47449650 0.60949748 -0.179598963
Michigan 2.10844115 -0.15539682 -0.38486858 0.102372019
Minnesota -1.69268181 -0.63226125 -0.15307043 0.067316885
Mississippi 0.99649446 2.39379599 0.74080840 0.215508013
Missouri 0.69678733 -0.26335479 -0.37744383 0.225824461
Montana -1.18545191 0.53687437 -0.24688932 0.123742227
Nebraska -1.26563654 -0.19395373 -0.17557391 0.015892888
Nevada 2.87439454 -0.77560020 -1.16338049 0.314515476
New Hampshire -2.38391541 -0.01808229 -0.03685539 -0.033137338
New Jersey 0.18156611 -1.44950571 0.76445355 0.243382700
New Mexico 1.98002375 0.14284878 -0.18369218 -0.339533597
New York 1.68257738 -0.82318414 0.64307509 -0.013484369
North Carolina 1.12337861 2.22800338 0.86357179 -0.954381667
North Dakota -2.99222562 0.59911882 -0.30127728 -0.253987327
Ohio -0.22596542 -0.74223824 0.03113912 0.473915911
Oklahoma -0.31178286 -0.28785421 0.01530979 0.010332321
Oregon 0.05912208 -0.54141145 -0.93983298 -0.237780688
Pennsylvania -0.88841582 -0.57110035 0.40062871 0.359061124
Rhode Island -0.86377206 -1.49197842 1.36994570 -0.613569430
South Carolina 1.32072380 1.93340466 0.30053779 -0.131466685
South Dakota -1.98777484 0.82334324 -0.38929333 -0.109571764
Tennessee 0.99974168 0.86025130 -0.18808295 0.652864291
Texas 1.35513821 -0.41248082 0.49206886 0.643195491
Utah -0.55056526 -1.47150461 -0.29372804 -0.082314047
Vermont -2.80141174 1.40228806 -0.84126309 -0.144889914
Virginia -0.09633491 0.19973529 -0.01171254 0.211370813
Washington -0.21690338 -0.97012418 -0.62487094 -0.220847793
West Virginia -2.10858541 1.42484670 -0.10477467 0.131908831
Wisconsin -2.07971417 -0.61126862 0.13886500 0.184103743
Wyoming -0.62942666 0.32101297 0.24065923 -0.166651801
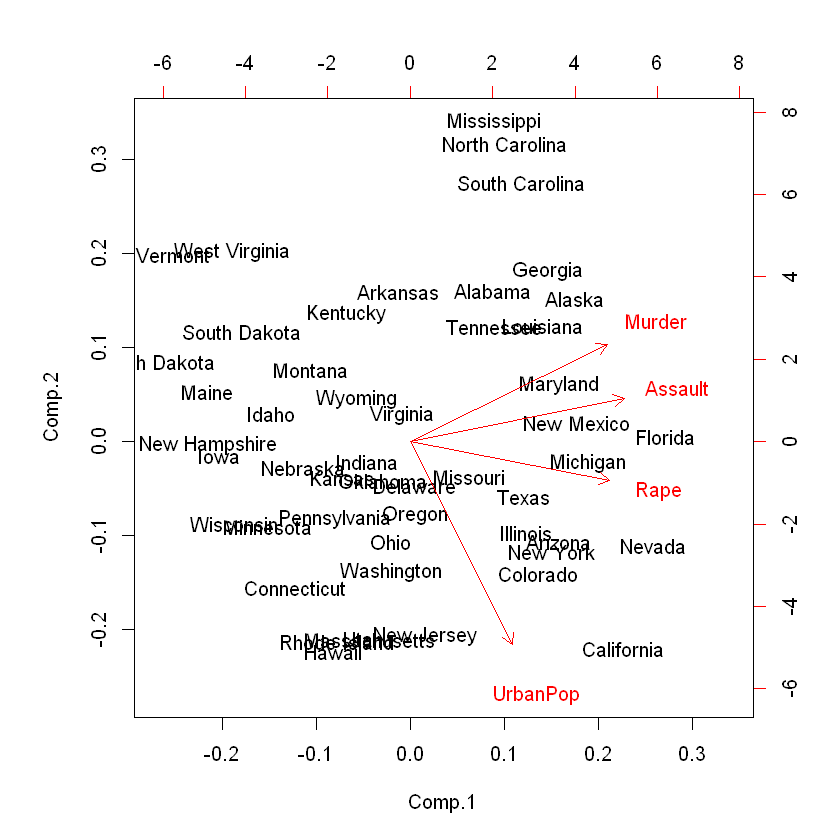
바이플롯(bibplot)은 관측치들을 첫 번째와 두 번째 주성분의 좌표에 그린 그림 출력
Comp1 이 Assault, Murder, Rape와 비슷한 방향을 가지고, UrbanPop과 방향이 수직에 가까운 것으로 보아 첫 번째 주성분이 주로 Assault, Murder, Rape 변수들에 대해 상대적으로 큰 가중치를 적용하여 계산된 것을 알 수 있음.
Comp2 이 UrbanPop와 상대적으로 평행하기 때문에 다른 변수들에 비해 UrbanPop의 영향을 크게 받아 구성된 것으로 보임.
즉, 첫 번째 주성분의 값이 작을수록 세 가지 범죄 발생율이 큰 주이고, 두 번째 주성분 값이 작을수록 도심인구 비율이 큰 주라고 해석 할 수 있음.
biplot(fit)
제4절 시계열 예측
1.정상성(Stationary)
시간의 흐름에 따라서 관측된 데이터를 시계열자료(Time-series Data)라고 함.
시계열분석(Time Series Analysis)을 위해서는 정상성(Stationary)을 만족해야 함.
정상성은 시점에 상관없이 시계열의 특성이 일정하다는 것을 의미함.
- 정상성 만족 조건
1) 평균이 일정하다.
2) 분산이 시점에 의존하지 않는다.
3) 공분산은 단지 시차에만 의존하고 시점 자체에는 의존하지 않는다.
위에서 정의한 정상성 만족 조건을 하나라도 만족하지 못하는 경우의 시계열 자료를 비정상 시계열이라고 부름.
대부분의 시계열 자료는 비정상 시계열 자료임. 비정상 시계열 자료는 정상성을 만족하도록 데이터를 정상 시계열 자료로 만든 후에 시계열 분석을 수행함.
따라서 주어진 시계열 자료가 정상성을 만족하는지 판단하는 과정이 필요함. 가장 먼저 시계열 자료 그림을 통해서 자료의 이상점(Outlier)과 개입(Intervention)을 살피고, 정상성 만족 여부와 개략적인 추세 유무를 관찰함.
이상점의 경우 일반적으로 해당 이상값을 제거하고, 개입의 경우 회귀분석을 수행하면 됨.
추세를 보이는(평균이 일정하지 않은) 경우에는 차분(Difference)을 통해 비정상 시계열을 정상 시계열로 바꾸고, 시간에 따라 분산이 일정하지 않은 경우에는 변환(Transformation)을 통해서 정상 시계열로 바꿀 수 있음.
차분이란 현 시점의 자료값에서 전 시점의 자료값을 빼는 것을 말함. 일반적인 차분은 현재 시점에서 바로 전 시점의 자료값을 빼는 것을 말하며, 여러 시점 전의 자료를 빼는 것을 계절차분(Seasonal Difference)이라고 함. 계절성을 갖는 비정상 시계열을 정상 시계열로 바꿀 때 계절차분을 사용함.
2. 시계열 모형
자기회귀 모형(AR모형)
자기회귀모형(Autoregressive model)은 현 시점의 자료가 p 시점 전의 유한개의 과거 자료로 설명될 수 있다는 의미이며 AR(p) 모형이라 함.
Zt = Φ1 * Zt-1 + Φ2 *Zt-2 + ... + Φp * Zt-p + at
at : 백색잡음과정(White Noise Process, 대표적 정상 시계열), 시계열 분석에서 오차항을 의미함.
at는 독립이고 같은 분포를 따르며 평균이 0이고 분산이 σa^2인 확률변수
<자기회귀모형 식별>
자기상관함수(ACF, Auto-Correlation Function), 부분자기상관함수(PACF, Partial Auto-Correlation Function)
일반적으로 자기회귀모형은 자기상관함수는 시차가 증가함에 따라 점차적으로 감소하고,
부분자기상관함수는 p+1 시차 이후 급격히 감소하여 절단된 형태이며, 이를 AR(p) 모형이라고 판별함.
이동평균모형(MA모형)
시계열 자료를 모형화 하는데 자기회귀모형 다음으로 많이 쓰이는 모형이 이동평균모형(Moving Average Model)임.
Zt = at - θ1*at-1 - θ2*at-2 - ... - θp*at-p
이동평균모형은 현 시점의 자료를 유한개의 백색잡음의 선형결합으로 표현되었기 때문에 항상 정상성을 만족함.
때문에 이동평균모형은 정상성 가정이 필요없음.
1차 이동평균모형, MA(1) 모형은 가장 간단한 이동평균모형으로 같은 시점의 백색잡음과 바로 전 시점의 백색잡음의 결합으로 이루어진 모형임.
<이동평균모형 식별>
이동평균모형을 판단하기 위한 모형 식별은 자기회귀모형과 마찬가지로 자기상관함수와 부분자기상관함수를 이용하여 식별하게 됨. 이동평균모형은 자기회귀모형과 반대로 자기상관함수는 p+1 시차 이후 절단된 형태가 되고, 이때를 MA(p) 모형이라 볼 수 있음. 그리고 부분자기상관함수는 점차 감소하는 형태를 띄게 됨.
자기회귀누적이동평균모형(ARIMA 모형)
대부분의 많은 시계열 자료가 자기회귀누적이동평균모형(Autoregressive Integrated Moving Average Model)을 따름.
ARIMA 모형은 기본적으로 비정상 시계열 모형이기 때문에 차분이나 변환을 통해 AR 모형이나 MA 모형, ARMA 모형으로 정상화할 수 있음.
ARIMA(p, d, q) 모형은 차수 p,d,q의 값에 따라 모형의 이름이 다르게 됨.
차수 p는 AR 모형과 관련이 있고,
q는 MA 모형과 관련이 있는 차수임
d는 ARIMA에서 ARMA로 정상화할 때 몇 번 차분을 했는지를 의미함.
d=0이면 ARMA(p,q) 모형이라 부르고, 이 모형은 정상성을 만족함.
p=0이면 IMA(d,q) 모형이라 부르고, 이 모형을 d번 차분하면 MA(q) 모형이 됨.
q=0이면 ARI(p,d) 모형이며, 이를 d번 차분한 시계열 모형이 AR(p) 모형을 따르게 됨.
분해 시계열
분해 시계열이란 시계열에 영향을 주는 일반적인 요인을 시계열에서 분리해 분석하는 방법을 말하며
회귀분석적인 방법을 주로 사용하고 있음. 시계열을 구성하는 요소는 다음 4가지로 분류됨.
1) 추세요인
자료의 그림을 그렸을 때 그 형태가 오르거나 내리는 추세를 따르는 경우가 있음.
물론 선형적으로 추세가 있는 것 이외에도 이차식의 형태를 취하거나 지수적 형태를 취할 수도 있는데,
이렇게 자료가 어떤 특정한 형태를 취할 때 추세요인(Trend factor)이 있다고 함.
2) 계절요인
요일마다 반복되거나 일년 중 각 월에 의한 변화, 사분기 자료에서 각 분기에 의한 변화 등
고정된 주기에 따라 자료가 변화하는 경우가 있음. 이렇게 고정된 주기에 따라 자료가 변화할 경우
계절요인(Seasonal factor)이 있다고 함.
3) 순환요인
명백한 경제적이나 자연적인 이유가 없이 알려지지 않은 주기를 가지고 변화하는 자료가 있음.
이와 같이 알려지지 않은 주기를 가지고 자료가 변화할 때 순환요인(Cyclical factor)이 있다고 함.
4) 불규칙요인
위 세 가지의 요인으로 설명할 수 없는 회귀분석에서 오차에 해당하는 요인을 불규칙요인(Irregular factor)라고 함.
분해 시계열 분석법에서는 각 구성요인을 정확하게 분리하는 것이 중요함. 그러나 각 요인을 정확하게 분리하는 것은
그리 쉽지 않음. 또한 분해 시계열 방법은 이론적인 약점이 있는 것으로도 알려져 있음.
하지만 경제학자들이나 조사통계학자들은 이러한 약점에도 널리 사용하고 있으며, 실제로 경제 분석이나 예측에서
이 방법은 성공적으로 사용되고 있음. 분해식의 일반적 정의는 다음과 같음.
Zt = f(Tt,St,Ct,It)
Tt : 경향(추세) 요인
St : 계절요인
Ct : 순환요인
It : 불규칙요인
Zt : 시계열 값
f : 미지의 함수
3. 실습
시계열 자료
1) 시계열 자료 불러오기
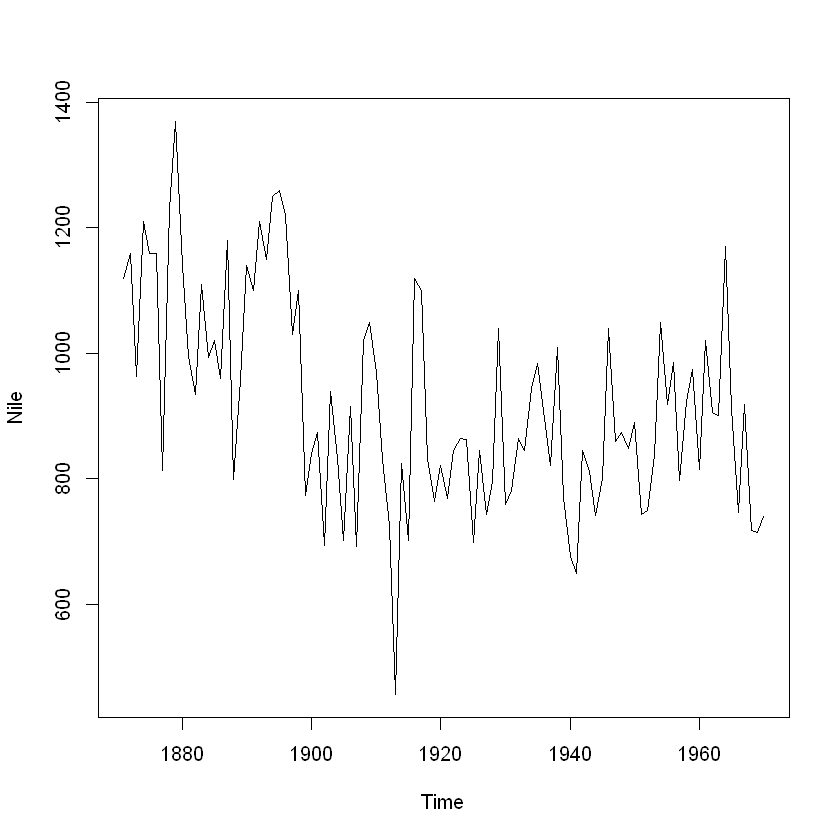
(예제1) Nile 데이터
1871~1970 아스완 댐에서 측정한 나일강의 여난 유입량에 관한 시계열 데이터
데이터 자체가 시계열 자료 형식인 ts 클래스를 갖기 때문에 따로 설정할 필요는 없음.
다만, 일반 데이터셋을 시계열 자료 형식으로 변환하려면 ts 함수를 사용하면 됨.
data(Nile)
print(Nile)
Time Series:
Start = 1871
End = 1970
Frequency = 1
[1] 1120 1160 963 1210 1160 1160 813 1230 1370 1140 995 935 1110 994 1020
[16] 960 1180 799 958 1140 1100 1210 1150 1250 1260 1220 1030 1100 774 840
[31] 874 694 940 833 701 916 692 1020 1050 969 831 726 456 824 702
[46] 1120 1100 832 764 821 768 845 864 862 698 845 744 796 1040 759
[61] 781 865 845 944 984 897 822 1010 771 676 649 846 812 742 801
[76] 1040 860 874 848 890 744 749 838 1050 918 986 797 923 975 815
[91] 1020 906 901 1170 912 746 919 718 714 740
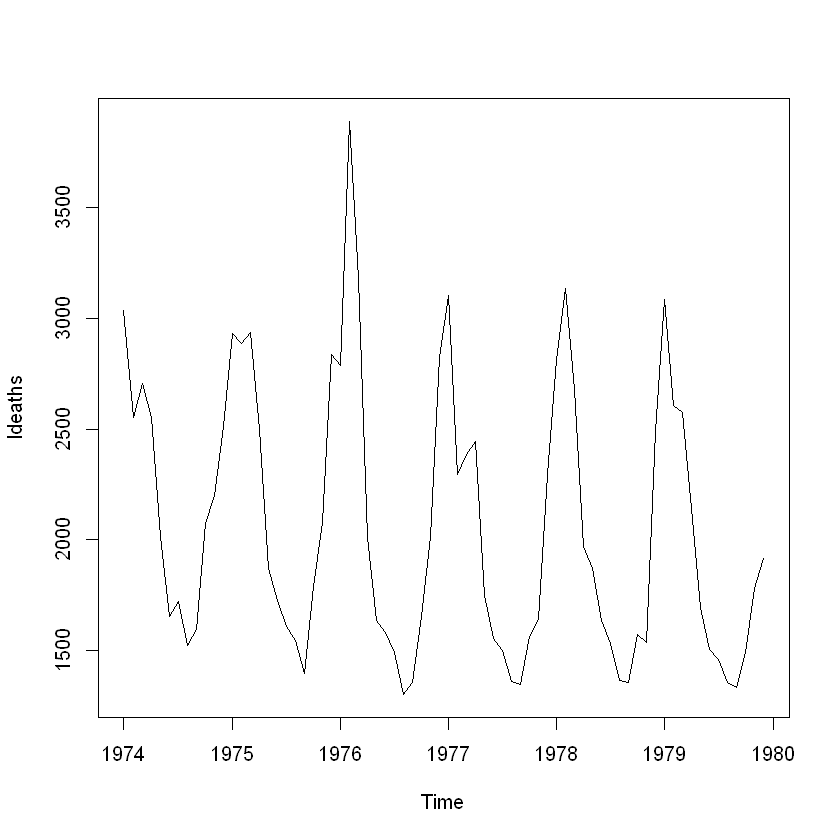
(예제2) ldeaths 데이터
1974~1979 영국 내의 월별 폐질환 사망자에 관한 시계열 데이터
*mdeath는 남성, fdeath는 여성에 관한 폐질환 사망자 데이터임.
data(ldeaths)
print(ldeaths)
Warning message in data(ldeaths):
"data set 'ldeaths' not found"
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1974 3035 2552 2704 2554 2014 1655 1721 1524 1596 2074 2199 2512
1975 2933 2889 2938 2497 1870 1726 1607 1545 1396 1787 2076 2837
1976 2787 3891 3179 2011 1636 1580 1489 1300 1356 1653 2013 2823
1977 3102 2294 2385 2444 1748 1554 1498 1361 1346 1564 1640 2293
1978 2815 3137 2679 1969 1870 1633 1529 1366 1357 1570 1535 2491
1979 3084 2605 2573 2143 1693 1504 1461 1354 1333 1492 1781 1915
2) 그림 고찰
# 나일강 연간 유입량 시계열 그림
# 비계절성을 띄는 데이터. 평균이 변화하는 추세를 보이므로 정상성 만족하지 못함.
plot(Nile)
# 폐질환 사망자 시계열 그림
# 년도 별로 계절성을 띄고 있는 것으로 보임. 매 년 일정 주기별로 사망자 수가 늘었다 줄었다 하는 경향을 보임
plot(ldeaths)
3) 분해 시계열
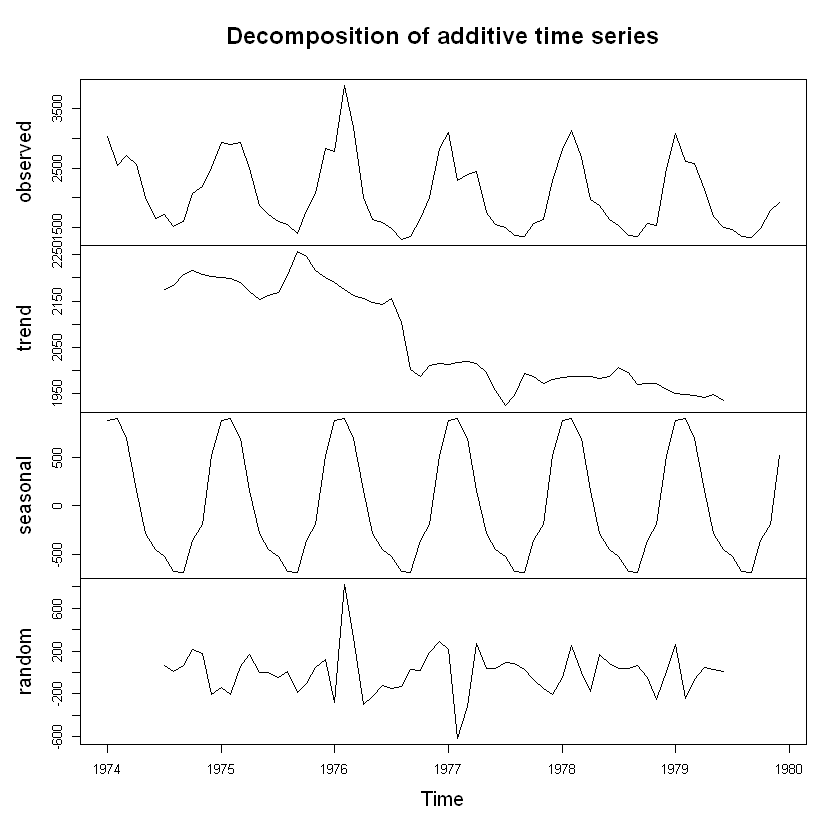
그림 고찰을 통해서 봤을 때 영국 내 폐질환 사망자 데이터는 계절성을 띄는 시계열 자료인 것으로 봄.
매년 4분기에 사망자수가 급증했다가 2분기에 급격히 감소하는 모습을 보임.
계절성을 띄는 시계열 자료는 추세요인, 계절요인, 불규칙요인으로 구성됨.
R에서 decompose 함수를 사용하면 시계열 자료를 4가지 요인으로 분해할 수 있음.
ldeaths.decompose = decompose(ldeaths)
print(ldeaths.decompose$seasonal)
Jan Feb Mar Apr May Jun Jul
1974 873.7514 896.3347 687.5431 156.5847 -284.4819 -440.0236 -519.4236
1975 873.7514 896.3347 687.5431 156.5847 -284.4819 -440.0236 -519.4236
1976 873.7514 896.3347 687.5431 156.5847 -284.4819 -440.0236 -519.4236
1977 873.7514 896.3347 687.5431 156.5847 -284.4819 -440.0236 -519.4236
1978 873.7514 896.3347 687.5431 156.5847 -284.4819 -440.0236 -519.4236
1979 873.7514 896.3347 687.5431 156.5847 -284.4819 -440.0236 -519.4236
Aug Sep Oct Nov Dec
1974 -669.8736 -678.2236 -354.3069 -185.2069 517.3264
1975 -669.8736 -678.2236 -354.3069 -185.2069 517.3264
1976 -669.8736 -678.2236 -354.3069 -185.2069 517.3264
1977 -669.8736 -678.2236 -354.3069 -185.2069 517.3264
1978 -669.8736 -678.2236 -354.3069 -185.2069 517.3264
1979 -669.8736 -678.2236 -354.3069 -185.2069 517.3264
폐질환 사망자 시계열 분해 그림
plot(ldeaths.decompose)
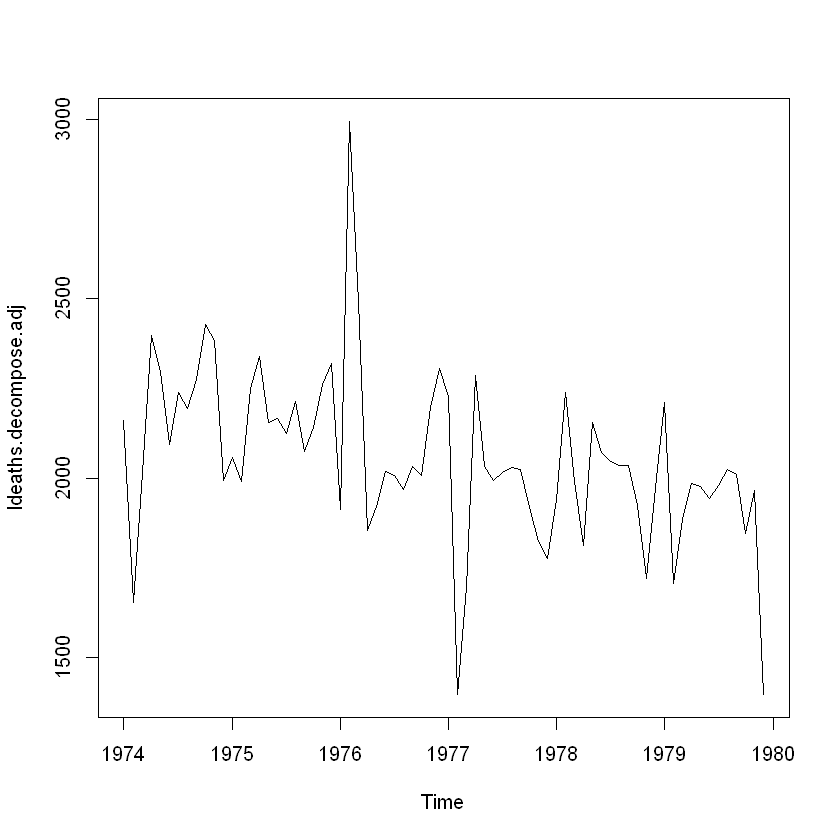
원 시계열 자료에서 계절요인 제거하기
계절성을 띄는 시계열 자료는 계절요인을 추정해 그 값을 원 시계열자료에서 빼면 적절하게 조정할 수 있음.
ldeaths.decompose.adj = ldeaths - ldeaths.decompose$seasonal
plot(ldeaths.decompose.adj)
4) ARIMA 모형
차분
나일강 연간 유입량 데이터는 그림으로 고찰해보았을 때 시간에 따라 평균이 일정하지 않은 비정상 시계열 자료였음. 따라서 diff 함수를 사용하여 차분을 함.
Nile.diff1 = diff(Nile, differences = 1)
plot(Nile.diff1)
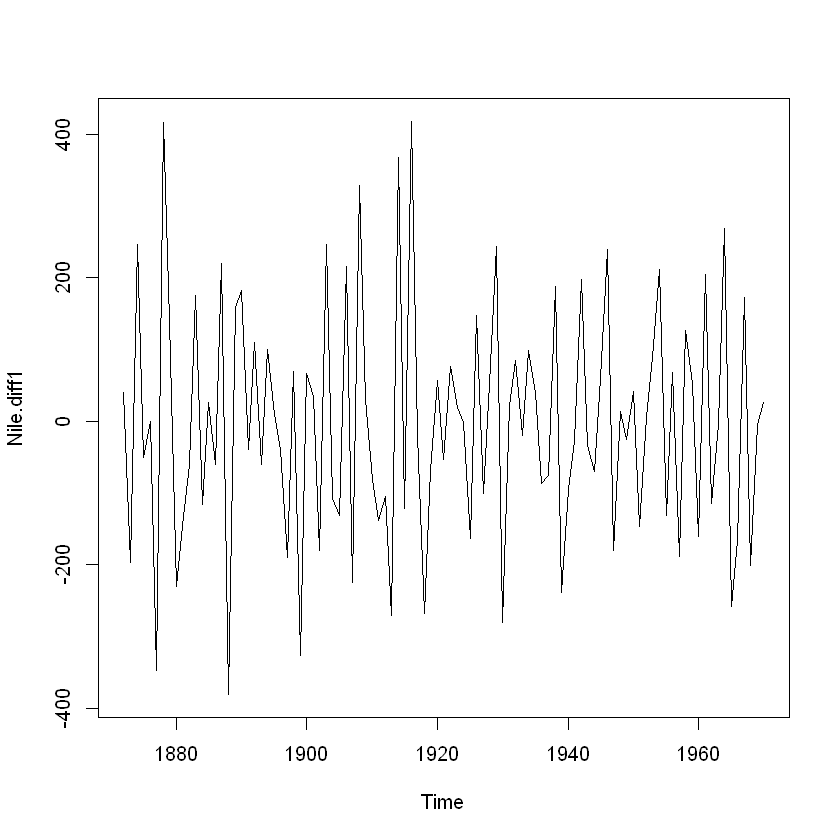
1번 차분한 결과로는 아직 평균이 일정하지 않아 보임. 차분을 2번 한 결과는 아래와 같음.
Nile.diff2 = diff(Nile, differences = 2)
plot(Nile.diff2)
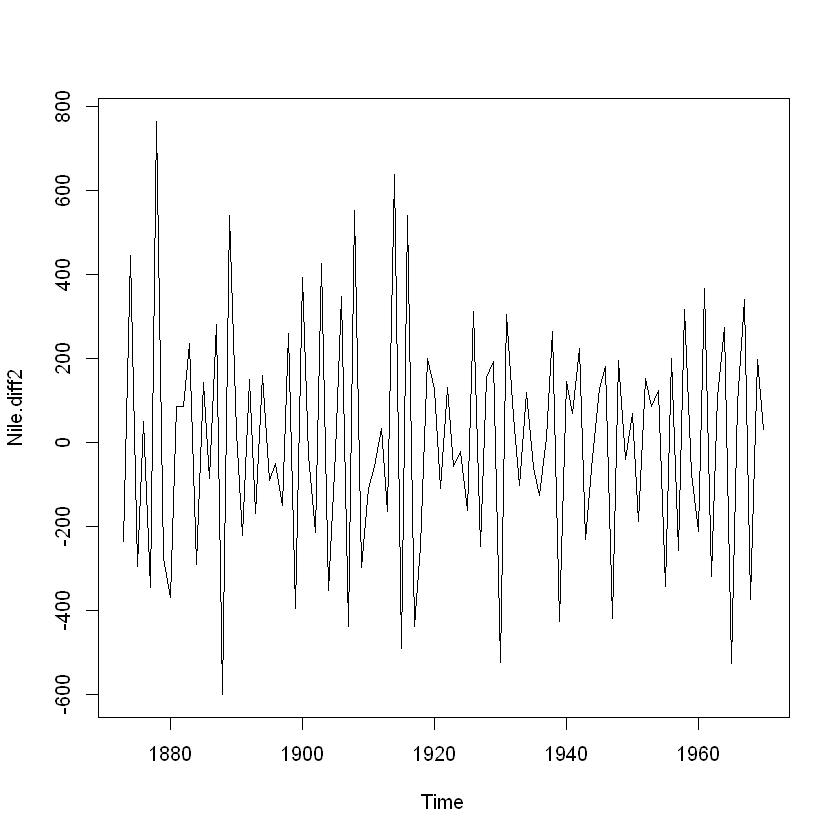
위 그림은 2번 차분한 결과로 시간이 지남에 따라 평균과 분산이 어느 정도 일정한 정상성을 만족하는 것으로 보임.
ARIMA 모형 적합 및 검정
자기상관함수와 부분자기상관함수를 통해 ARIMA 모형을 적합한 후에 최종 모형을 결정할 수 있음.
자기상관함수를 살펴보기 위해 acf 함수를 사용하여 2차 차분을 한 나일강 연간 유입량 시계열 자료의 자기상관함수 그래프를 그려보면 다음과 같음.
acf(Nile.diff2, lag.max=20)
acf(Nile.diff2, lag.max=20, plot=FALSE)
Autocorrelations of series 'Nile.diff2', by lag
0 1 2 3 4 5 6 7 8 9 10
1.000 -0.626 0.100 0.067 -0.072 0.017 0.074 -0.192 0.245 -0.079 -0.153
11 12 13 14 15 16 17 18 19 20
0.183 -0.106 0.062 0.010 -0.096 0.134 -0.134 0.091 -0.030 0.003
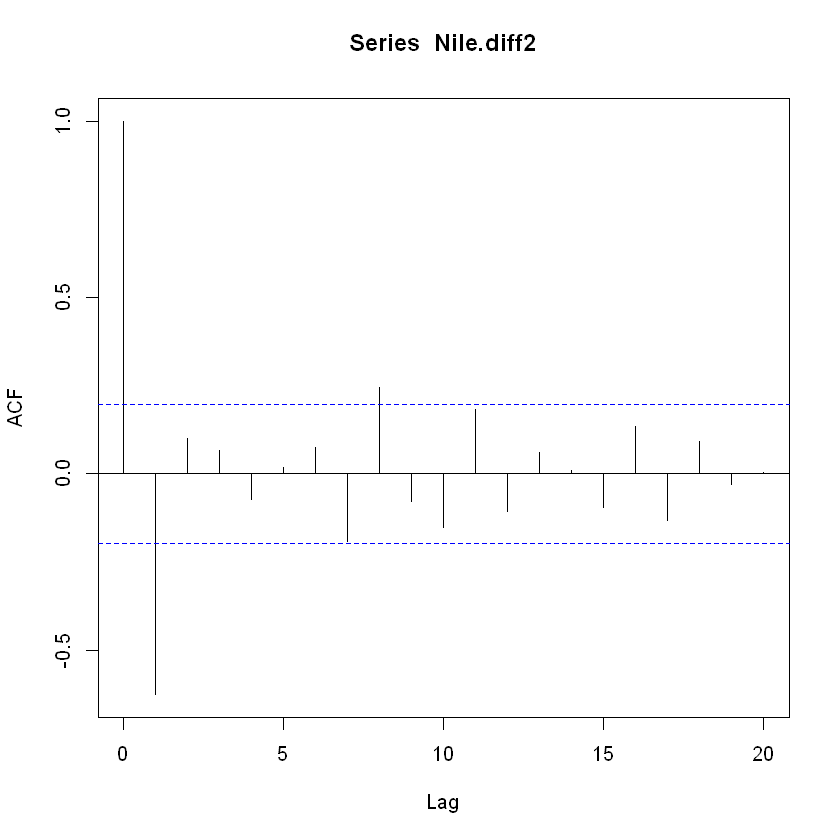
acf 함수의 lag 개수 20개로 설정했음. lag 개수를 너무 많이 설정하면 자기상관함수 그래프를 보고 모형 식별을 위한 판단이 힘들기 때문에 적절한 값을 선택함.
위 결과 자기상관함수가 lag=1, 8을 제외하고 모두 신뢰구간 안에 있는 것을 확인할 수 있음.
다음으로 부분자기상관함수 그래프를 그려보면 아래와 같음.
pacf(Nile.diff2, lag.max = 20)
pacf(Nile.diff2, lag.max = 20, plot=FALSE)
Partial autocorrelations of series 'Nile.diff2', by lag
1 2 3 4 5 6 7 8 9 10 11
-0.626 -0.481 -0.302 -0.265 -0.273 -0.112 -0.353 -0.213 0.038 -0.120 -0.117
12 13 14 15 16 17 18 19 20
-0.197 -0.132 -0.055 -0.109 0.022 -0.184 -0.067 -0.037 -0.024
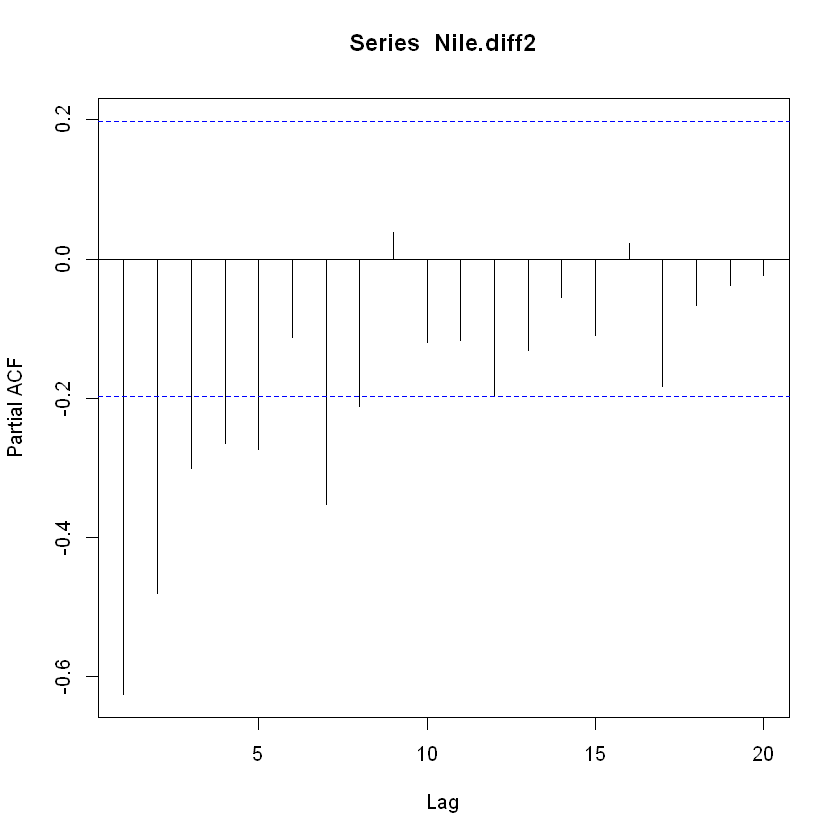
부분자기상관함수가 lag=1~8에서 신뢰구간을 넘어서 음의 값을 가지고, lag=9에서 절단된 것을 볼 수 있음.
이와 같이 자기상관함수와 부분자기상관함수의 그래프를 종합해보면 다음과 같은
ARMA 모형이 존재하게 됨.
- ARMA(8,0) : 부분자기상관함수 그래프에서 lag=9에서 절단되었음
- ARMA(0,1) : 자기상관함수 그래프에서 lag=2에서 절단되었음
- ARMA(p,q) : AR 모형과 MA 모형을 혼합하여 모형을 식별하고 결정해야 함
어떤 모형을 선택해야하느냐 하는 문제는 생각처럼 쉽지 않음. 모수가 많다면 모형을 설명하는 설명력이
커지겠지만, 모형이 복잡하고 이해하기 어려움. 반대로, 모수가 적은 모형을 선택한다면 모형이 단순하고
이해하기 쉽지만, 모형을 설명하는 설명력이 상대적으로 낮아질 수밖에 없음.
본 예제에서는 forecast 패키지에 있는 auto.arima 함수를 사용하여 적절한 ARIMA 모형을 결정하도록 할 것임.
forecast 패키지 - auto.arima 함수
install.packages('forecast')
library(forecast)
auto.arima(Nile)
Installing package into 'C:/Users/wooil/Documents/R/win-library/3.6'
(as 'lib' is unspecified)
package 'forecast' successfully unpacked and MD5 sums checked
The downloaded binary packages are in
C:\Users\wooil\AppData\Local\Temp\RtmpoVx66K\downloaded_packages
Registered S3 method overwritten by 'xts':
method from
as.zoo.xts zoo
Registered S3 method overwritten by 'quantmod':
method from
as.zoo.data.frame zoo
Registered S3 methods overwritten by 'forecast':
method from
fitted.fracdiff fracdiff
residuals.fracdiff fracdiff
Series: Nile
ARIMA(1,1,1)
Coefficients:
ar1 ma1
0.2544 -0.8741
s.e. 0.1194 0.0605
sigma^2 estimated as 20177: log likelihood=-630.63
AIC=1267.25 AICc=1267.51 BIC=1275.04
auto.arima 함수를 사용하여 나일강의 연간 유입량 시계열 자료에 적절한 모형은 ARIMA(1,1,1) 모형으로 결정된 것을 알 수 있음.
ARIMA 모형을 이용한 예측
시계열 자료에 대해 적절한 ARIMA 모형이 결정되었다면, ARIMA 모형을 통해 미래의 수치 값을 예측할 수 있음.
앞서 나일강 연간 유입량 시계열 자료의 모형은 ARIMA(1,1,1) 모형으로 결정되었음.
이 시계열 자료를 ARIMA(1,1,1) 모형에 적합함.
Nile.arima = arima(Nile, order=c(1,1,1))
Nile.arima
Call:
arima(x = Nile, order = c(1, 1, 1))
Coefficients:
ar1 ma1
0.2544 -0.8741
s.e. 0.1194 0.0605
sigma^2 estimated as 19769: log likelihood = -630.63, aic = 1267.25
데이터를 모형에 적합한 후 forecast 패키지의 forecast 함수를 사용하여 미래의 수치 값을 예측함.
h=10은 10개 년도만 예측한다는 의미임.
Nile.forecasts = forecast(Nile.arima, h=10)
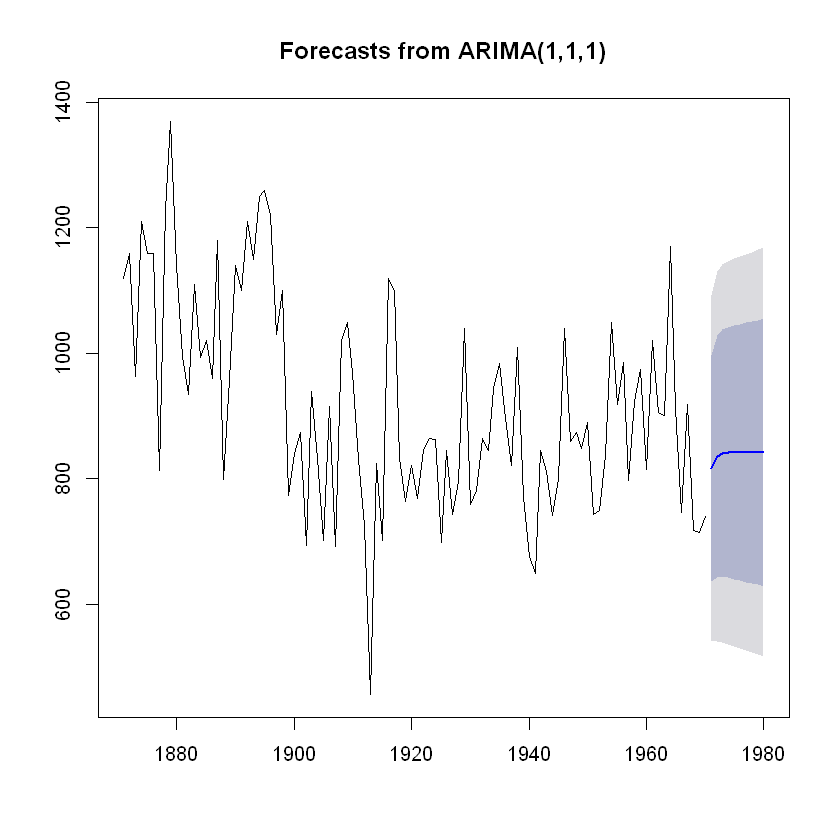
나일강 유입량 데이터 예측 그래프
plot(Nile.forecasts)
댓글남기기